R语言

1. t检验主要有三类：单一样本t检验、独立样本t检验、配对样本t检验。

2. 独立样本t检验是一种组间检验方法，它的H0是两组样本间的平均数没有差异。

3. 配对样本t检验是一种组内检验方法，它可以检测同一对象的不同水平或不同时期的均数有没有差异。

4. 在R中我们使用t.test( )函数即可完成t检验，其中paired=TRUE使用的是配对样本t检验，paired=FALSE使用的是独立样本t检验。

5. p值越小并不意味着差距越大，而是意味着我们有越有充足的理由拒绝H0。

6. 报告t检验时，要同时报告均数和标准差，以及t检验的自由度和p值。
   

R: The R Project for Statistical Computing

https://www.r-project.org/

RStudio:

https://rstudio.com/

我们上一期提到了t检验可以用来分析两组不同样本之间的平均数差异情况，但是往往我们的语言研究并不局限于“两组”样本，更多时候是两组以上的样本量。如果我们继续使用t检验，分别进行配对比较（如样本1、2、3两两比较），这也是可以的，但是多次比较会增加犯Type I error的概率。一个t检验犯Type I error的概率是5%，进行3次t检验，这个概率会增加到15%,它的计算方法如下，被称为多重比较谬误(family-wise error)。如果比较的组数n增加，犯错的概率也会增加。

多重比较谬误

那如果我们想要比较多个组之间的差异是否显著，显然使用t检验已经不足够了，这时候我们需要换另一种检验方法，这种方法叫做方差检验(ANalysis Of VAriance，简称ANOVA)，它可以处理两个及以上的处理，同时比较多个组之间的平均数差异。根据不同的实验设计，我们可以有不同的方差检验方法，具体如下图所示。

莱顿大学Statistics in Linguistics课程讲义

根据方差检验的定义，我们可以对方差分析的零假设和备择假设进行如下的陈述。

H₀：μ₁=μ₂=μ₃=…=μ_n

H₁：至少有一个平均数与其他数值不一样

注意，这里的备择假设只是一种描述，根据研究目的的不同，你也可以描述为某两个或多个相同，某一个或多个与其他不同。在做好假设陈述后，就需要进行统计量的计算。在介绍统计量之前，我们首先要明确一点。t检验中t统计量是让平均数差除以估计误差值得到，ANOVA其实与之类似，不同的是分子上我们使用的差异值。因为我们是进行两个以上的样本的比较，那么这时候我们就不可能计算“平均数差”——因为你没办法决定到底以哪两组的平均数差来做差异值，因此这时候我们使用离均差平方和(Sum of Squares，简称SS)来做我们的差异检测量，它可以描述样本值到平均值偏移程度，从而测量样本平均数之间的差异。

在方差计算中可以看到SS的计算方式

对于ANOVA而言，它会把总平方和(Total Sum of Squares，简写SS_T)分为两部分，一部分是与实验中我们操纵的自变量有关的组间平方SS_b，一部分是与随机误差产生的组内不同观测值的组内平方SS_w。所谓的总平方和就是组间平方和与组内平方和相加，借此我们便可以计算出组间均方差MSb和组内均方差MS_w。通俗来说，组间均方差就是因为我们要观察的因素所引起的差异，而组内均方差就是具体数据的差异。

比如，我要考察少年、中年、老年三个年龄段的元音/a/的F1有没有差异，那么组间均方差就是少年、中年、老年三个组F1均数算得的方差，少年内部各发音人因为个体的不同（随机抽样误差）而出现的数据的不同，这个算出来的方差就是组内均方差。它是在同一个组内，该组内的处理效应是一致的，因此我们说组间均方差包含着由处理效应引起的差异和偶然引起的差异（随机抽样），而组内只有偶然引起的差异。

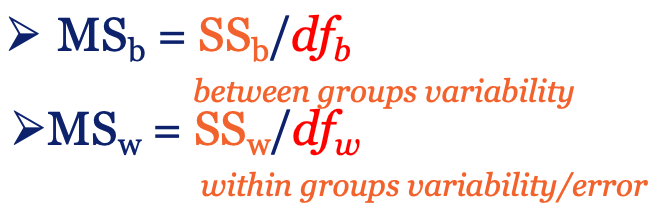
组间均方差与组内均方差的计算公式

得到组间均方差和组内均方差后，我们就可以计算方差分析的统计量了，这个统计量被称作F统计量(F-statistic)，得到的值就是F值，F统计量是用来评估变异性的显著性差异，它的计算方式是组间均方差与组内均方差的比值，因此在报告的时候你会看到，F值的括号内有两个数值，实际上它分别代表了组间的自由度和组内的自由度。

F值计算

最后我们要提一句方差分析的基本逻辑。同t检验相似，方差分析同样需要数据服从正态分布，另外它要求方差是齐性的，因此这两点同样是需要我们在进行方差分析前进行比较分析的。

下面我们开始正式的方差分析，首先我们介绍单因素方差分析(one-way ANOVA)，注意的是这里的单因素方差分析不是重复测量的，第三部分我们会介绍组内实验设计(within-subject design)中的重复测量下的方差分析。

莱顿大学Statistics in Linguistics课程讲义

对于单因素方差分析而言，它实际上是对三组及以上数据的均数是否具有差异进行检测的，某种意义上它是对独立样本t检验的拓展。正如我们上面提到的，在单因素方差分析中，我们对假设的陈述是有关于均值的情况。

        H0：μ1=μ2=μ3=…=μn

        H1：并不是所有的均数都相等

在做完假设后，我们就开始计算相关统计量，得到F值。与t检验一样，我们同样需要找到F临界值F_critical，从而判断我们的分析结果是否具有显著性差异。之前同样我们需要翻阅F值的表格，现在我们可以使用R中的相关函数来实现对数据的方差分析。我们常见的方差分析函数有aov( )函数、Anova( )函数(car包)、ezANOVA( )函数(ez包)三个，这三种函数各有利弊，语句也不一样。今天我们介绍aov( )函数，比较简单。为了方便，我们直接调用R中自带的数据集PlantGrowth。

PlantGrowth函数

使用aov( )函数做方差分析前，我们照例需要对数据是否是正态分布进行检测，这个内容在之前的推论性统计一文中介绍过，我们使用shapiro.test( )函数检测发现group中的三组样本均是来自正态分布的总体的数据。接下来我们需要对数据的方差齐性进行检验，这也是我们做方差检验最关键的一步。我们调用bartlett.test( )函数观察p值，这里的H0是不同组数据间方差相等，我们通过检测可以看到p>.05，因此接受H0，说明方差是齐性的。

方差齐性检验

现在，我们可以调用aov( )函数进行分析了。同方差齐性检验的语句类似，我们只需要告诉R是哪两个变量之间进行比较分析即可，最后使用summary( )函数可以看到，p<.05，因此是具有显著性差异的，那么我们需要进行如下的报告：

    根据单因素方差分析，不同组间的植物生长情况在重量上具有显著性差异，F(2, 27)=4.846，p=.01。

注意，这里的方差分析我们只能说明，至少存在一个样本的均数与其他样本不同，但究竟是哪个出现了显著性差异，这时候我们需要进行事后检验(post hoc analysis)。事后检验的具体算法有多种，比如Tukey's test，Scheffe's test等，比如使用Tukey's test，我们需要加载stats包然后调用TukeyHSD( )函数即可。

单因素方差分析结果

今天我们首先讲了单因素方差分析的方法，那么对于重复测量的分析该如何进行，以及双因素和多因素的方差分析，我们又该怎么解决？下一期我们将着重介绍常用到的这些方差分析方法。