15.2.1非标准化回归系数（Unstandardized regression coefficients）

我们也可以根据非标准化或标准化回归系数计算Hedges'g（Lipsey and Wilson 2001）。

对于非标准化的回归系数，我们可以使用esc_B函数和以下参数：

·b：非标准化系数b（the “treatment” predictor）。

·sdy：因变量y（例如，结果变量）的standard deviation。

·grp1n：第一组参与者的数量。

·grp2n：第二组参与者的数量。

·es.type：我们想要计算的效果量度。在我们的例子中是“g”。但是我们也可以使用“d”来计算Cohen’s d。

代码示例如下：

esc_B(b=3.3,sdy=5,grp1n = 100,grp2n = 150,es.type = "g")
## ## Effect Size Calculation for Meta Analysis## ##      Conversion: unstandardized regression coefficient to effect size Hedges' g##     Effect Size:   0.6941##  Standard Error:   0.1328##        Variance:   0.0176##        Lower CI:   0.4338##        Upper CI:   0.9544##          Weight:  56.7018

15.2.2标准化回归系数（standardized regression coefficients）

对于非标准化的回归系数，我们可以使用esc_beta函数与以下参数：

·beta：标准化系数β（the “treatment” predictor）。

·sdy：因变量y（例如，结果变量）的标准偏差（standard deviation）。

·grp1n：第一组参与者的数量。

·grp2n：第二组参与者的数量。

·es.type：我们想要计算的效果量度。在我们的例子中是“g”。但是我们也可以使用“d”来计算Cohen’s d。

代码示例如下：

esc_beta(beta=0.7, sdy=3, grp1n=100, grp2n=150, es.type = "g")
## ## Effect Size Calculation for Meta Analysis## ##      Conversion: standardized regression coefficient to effect size Hedges' g##     Effect Size:   1.9868##  Standard Error:   0.1569##        Variance:   0.0246##        Lower CI:   1.6793##        Upper CI:   2.2942##          Weight:  40.6353

要计算卡方检验中的比值比或任何其他类型的效应大小度量，我们可以使用带有以下参数的esc_chisq 函数：

• chisq: 卡方值 (或仅用 参数p)

• p: 卡方p值 或 phi 值 (或仅用 参数chisq)

• totaln: 总样本量

• es.type: 结果返回的效应量度 (在本例中用"cox.or"，即以Cox比列风险回归得到的比值比)

代码示例如下：

## ## Effect Size Calculation for Meta Analysis## ##      Conversion: chi-squared-value to effect size Cox odds ratios##     Effect Size:   2.9858##  Standard Error:   0.3478##        Variance:   0.1210##        Lower CI:   1.5101##        Upper CI:   5.9036##          Weight:   8.2667

我们可以根据两组单因素方差分析的F值推导出标准化平均差（SMD）。只要你找到F值对应的自由度（df），就可以检测这些方差分析结果。在两组的单因素方差分析中，自由度应该总是从1开始（比如 F1,147= 5.31）。这个转换的公式如下：

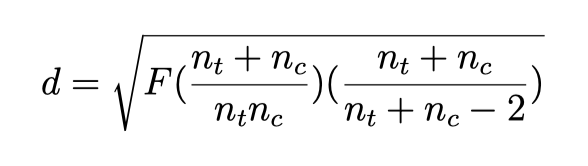
根据F值计算Hedges’g值，可以使用带有以下参数的esc_f函数：

• f: 方差分析的F值

• grp1n: 第一组的参与者人数

• grp2n: 第二组的参与者人数

• totaln: 总样本量（如果未报告各个组的人数）

• es.type: 我们要计算的效应量度。在本例中用 "g"。但是我们也可以使用 "d" 来计算Cohen’s d。

代码示例如下：

esc_f(f=5.04,grp1n = 519,grp2n = 528,es.type = "g")## ## Effect Size Calculation for Meta Analysis## ##      Conversion: F-value (one-way-Anova) to effect size Hedges' g##     Effect Size:   0.1387##  Standard Error:   0.0619##        Variance:   0.0038##        Lower CI:   0.0174##        Upper CI:   0.2600##          Weight: 261.1022

根据均值和标准误计算Hedges’g时，我们简单地利用了这样一个事实：当考虑样本量时，标准误不超过标准差。

我们可以使用带有以下参数的esc_mean函数，来计算Hedges’g值：

• grp1m: 第一组的均值

• grp1se: 第一组的标准误

• grp1n: 第一组的样本量大小

• grp2m: 第二组的均值

• grp2se: 第二组的标准误

• grp2n: 第二组的样本量大小

• es.type: 我们要计算的效应量度。在本例中用 "g"。但是我们也可以使用 "d" 来计算Cohen’s d。

代码示例如下：

esc_mean_se(grp1m = 8.5, grp1se = 1.5, grp1n = 50,  grp2m = 11, grp2se = 1.8, grp2n = 60, es.type = "g")## ## Effect Size Calculation for Meta Analysis## ##      Conversion: mean and se to effect size Hedges' g##     Effect Size:  -0.1998##  Standard Error:   0.1920##        Variance:   0.0369##        Lower CI:  -0.5760##        Upper CI:   0.1765##          Weight:  27.1366

对于被试人数相等的两组（n1=n2），我们可以利用下面的公式从点二列相关(the pointbiserial correlation)中得出标准化平均差（SMD）。

当被试数不相等时：

要将rpb值转化为Hedges’g值，我们可以使用带有以下参数的esc_rpb函数：

•r: r值，必须给出r或者它的p值

•p: 相关性p值，必须给出r或者它的p值

•grp1n: 第一组的被试人数

•grp2n: 第二组的被试人数

•totaln: 总样本量（如果未报告各个组的人数）

•es.type: 我们要计算的效应量度。在本例中用 "g"。但是我们也可以使用 "d" 来计算Cohen’s d。

代码示例如下：

esc_rpb(r = 0.25, grp1n = 99, grp2n = 120, es.type = "g")## ## Effect Size Calculation for Meta Analysis## ##      Conversion: point-biserial r to effect size Hedges' g##     Effect Size:   0.5170##  Standard Error:   0.1380##        Variance:   0.0190##        Lower CI:   0.2465##        Upper CI:   0.7875##          Weight:  52.4967

标准化平均差（SMD）也可以从独立样本t检验得出，公式如下：

要根据t检验计算Hedges’g值，我们可以使用带有以下参数的esc_t函数：

•t: t检验中的t值，必须给出t或者它的p值

•p:t检验中的p值，必须给出t或者它的p值

•grp1n: 第一组的被试人数

•grp2n: 第二组的被试人数

•totaln: 总样本量（如果未报告各个组的人数）

•es.type: 我们要计算的效应量度。在本例中用 "g"。但是我们也可以使用 "d" 来计算Cohen’s d。

代码示例如下：

esc_t(t = 3.3, grp1n = 100, grp2n = 150,es.type="g")## ## Effect Size Calculation for Meta Analysis## ##      Conversion: t-value to effect size Hedges' g##     Effect Size:   0.4247##  Standard Error:   0.1305##        Variance:   0.0170##        Lower CI:   0.1690##        Upper CI:   0.6805##          Weight:  58.7211

我们可以使用Hedges和Olkin的公式直接将Cohen’s d转化为Hedges’g：

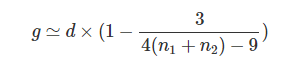
这可以在R中使用带有以下参数的hedges_g函数：

• d: Cohen’s d值

• totaln: 总样本量N

代码示例如下：

hedges_g(d = 0.75, totaln = 50)## [1] 0.7382199

许多随机对照试验不仅包括单个干预组和对照组，而且将两种或多种干预措施的效果与对照组进行了比较。在这种情况下，将一项研究中的干预组和对照组的所有条件进行比较，简单地纳入到一项元分析可能会很诱人。但是，研究人员应该放弃这种做法，因为这意味着对照组在元分析中被使用了两次，从而“双倍计算”（double-counting）了对照组的参与者。效应大小是相关的，不是独立的，双倍计算对照组是将其视为参与者源自于独立样本，这会导致分析单位误差 (unit-of-analysis error)。

有两种方法可以解决此问题：

拆分对照组的参与者人数N：在某种程度上控制分析单位误差 (unit-of-analysis error) 的一种方法是在两个干预组之间拆分对照组的参与者数量。因此，如果您的对照组有N = 50个参与者，则可以将对照组分为两个均值和标准偏差相同的对照组，每个组有N = 25个参与者。在此准备步骤之后，您可以计算每个干预组的效果大小。由于此过程只能部分消除分析单位误差，因此通常不建议这样做。但是，此程序的一大优点是它使研究部分之间的异质性研究成为可能。

另一个选择是把干预组的结果合并成一组，与对照组进行比较。尽管此过程存在实际操作的的局限性（有时，这意味着要把来自极其不同类型的干预组的结果合并为一组），但摆脱了分析单位误差的问题，因此从统计学的角度出发建议这样做。具体计算如下：

    合并效果大小（合并的均值，标准偏差和N），使用以下公式：

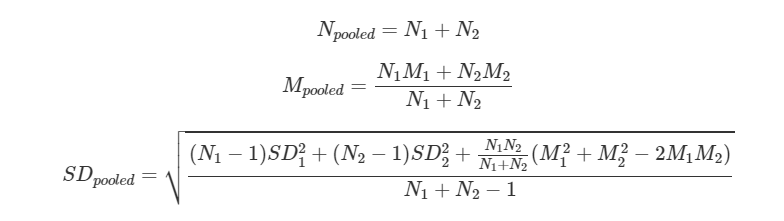
由于这些公式很长，您可以使用pool.groups函数，该函数会自动为您进行合并。该函数是dmetar软件包的一部分。如果已经安装了dmetar包，必须先将其加载到库中。

library(dmetar)

如果您不想使用dmetar包，则可以使用书中对应位置链接中的源代码。此案例中，R中没有此函数，因此我们必须通过将代码完整复制并粘贴到RStudio左下方窗格的控制台中。使用此功能需要指定以下参数：

•n1：第一组中的N

•n2：第二组中的N

•m1：第一组的平均值

•m2：第二组的平均值

•sd1：第一组的标准偏差

•sd2：第二个要素的标准偏差

代码示例如下：

pool.groups(n1=50,            n2=50,            m1=3.5,            m2=4,            sd1=3,            sd2=3.8)

如果一项研究有两个以上要合并的干预组（例如，四个组，具有三种不同的干预项目intervention arms），则可以先合并前两个干预组的效应量数据，然后跟来自第三组的数据再次进行合并。

可以将pool.groups的输出另存为一个对象，然后再使用$操作符，具体操作如下：

首先，合并第一和第二干预组。将输出另存为res。

res <- pool.groups(n1 = 50,                   n2 = 50,                   m1 = 3.5,                   m2 = 4,                   sd1 = 3,                   sd2 = 3.8)

    然后，使用保存在res中的合并数据与第三组中的数据合并，使用$运算符访问保存在res中的不同值。

pool.groups(n1 = res$Npooled,            n2 = 60,            m1 = res$Mpooled,            m2 = 4.1,            sd1=res$SDpooled,            sd2 = 3.8)

效应量如Cohen’s d或者Hedges’g很难从临床角度来解释。g=0.35对患者、医疗专业人员或其他利益相关者的影响究竟意味着什么？通过计算需要治疗的人数(NNT) ，有助于对该结果的理解，即为了避免一个额外的负面事件(如复发)或达到一个额外的正面事件(如症状缓解)，必须对多少额外的患者进行干预或治疗。有两种方法可以根据效应大小（如Cohen’s d或者Hedges’g）计算需要治疗的人数。

方法一：根据Kraemer和Kupfer(2006)，根据曲线下的面积(the Area Under the Curve，AUC)计算NNT。该面积表示接受治疗的患者比对照组患者获得更好结果的概率。这种方法允许直接根据d、g计算NNT，不需要任何额外的变量。

方法二：根据Furukawa，可以通过使用一个合理估计值CER根据d计算出NNT，大多数情况下CER是控制组的假设反应率（the assumed response rate in the control group）。

注：有研究表明，Furukawa的方法要比Kraemer 与 Kupfer的方法好(Furukawa and Leucht 2011)。如果可以假设一个合理的CER值，Furukawa的方法更好。

方法三：当使用事件数据时，首先计算CER或者实验组事件率（experimental group event rate），然后根据NNT的标准定义

15.10.1 NNT 函数

为了使用这三种方法计算NNT，可以使用NNT函数。该函数是dmetar包的一部分。如果您已经安装了软件包，那么您必须首先将其加载到库中。

library(dmetar)

如果您不想使用dmetar包，可以找到这个函数的源代码。通过将整个代码复制粘贴到RStudio左下方窗格的控制台中，然后点击Enter。

Kraemer 与 Kupfer 的方法

要使用Kraemer与Kupfer的方法，我们只需为函数提供效应量大小(d或g)。代码示例如下：

NNT(d = 0.245)## Kraemer & Kupfer's method used.## [1] 7.270711

Furukawa的方法

一旦输入CER值，Furukawa的方法就会被自动使用。代码示例如下：

NNT(d = 0.245, CER = 0.35)## Furukawa's method used.## [1] 10.61533

二进制事件数据（Binary event data）

使用二进制事件数据来直接计算NNT，只需要实验组event.e的事件率和实验组的总样本,n.e,以及对照组在event.c和n.c中的相同信息。代码示例如下：

NNT(event.e = 10, event.c = 20, n.e = 200, n.c = 200)## [1] 20

library(dmetar)

如果您不想使用dmetar包，可以找到这个函数的源代码，并将整个代码复制粘贴到RStudio左下方窗格的控制台，然后点击Enter。然后，使用该函数还需要esc包。

基于差异的效果量计算

例子：假设我们有一项研究，被试N=75，效应量d=0.71，p=0.013，标准误计算过程如下:

se.from.p(effect.size = 0.71,           p = 0.013,           N = 75,          effect.size.type= "difference")

基于比率的效应量计算

例子：假设我们有一项研究,200名被试报告效应量为OR=0.91与p=0.05,我们可以计算标准误如下:

se.from.p(effect.size = 0.91,           p = 0.05,           N = 200,          effect.size.type= "ratio")

从输出中可以看到，该函数自动计算了对数变换效应大小（the log-transformed effect size）和标准误,用到了metagen函数(参见第4.3.3 章)。