R语言

1. 相关是用来描述和测量两个变量之间关系的统计分析方法，很多情况下是对没有控制或操纵情况下变量的观察。

2. 根据关系的方向，相关可以分为正相关和负相关两种类型。以此，我们可以绘制出一条直线来预测。

3. 一个简单的线性回归由斜率和截距组成，记为Yi = b0 + b1Xi + εi,其中b0和b1被称为回归系数，εi被称为残差，是观测到的数据到回归线的距离。

4. 使用R2可以判断线性回归模型的拟合优度，范围在[0,1]浮动，越接近1说明拟合程度越好。

5. 在R中使用lm( )函数可以实现回归分析的建模，完成建模后使用summary( )函数查看建模结果，并使用anova( )函数与base model (null model)比较，如果有显著性差异，说明我们添加的因素对因变量有影响。

R: The R Project for Statistical Computing

https://www.r-project.org/

RStudio:

https://rstudio.com/

上一期我们介绍了最基础的线性回归方式，并了解到了lm( )函数的使用方法。通过写相关代码我们了解到，线性回归分析本质上是不断添加参数以和无参数的null model (base model)进行比较，从而检验自变量是否对因变量有影响。与其他假设检验一样，当你在进行线性回归分析前，要注意它们能顺利进行的三个前提假设，包括线性(linearity)、残差正态性(normality of residuals)、残差的方差齐性(homoscedasticity of residuals)，下面我们对这三个方面进行解释。

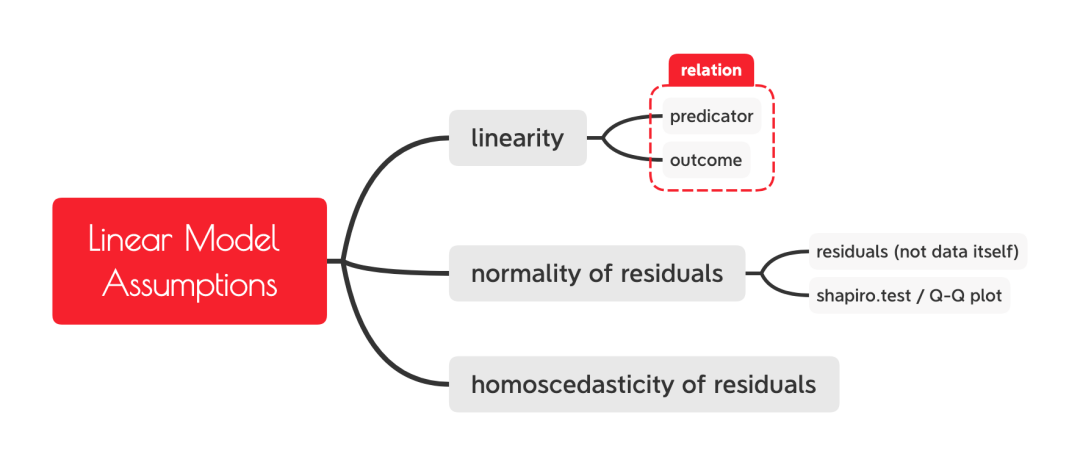
线性回归分析的三个假设

首先是线性，实际上这个问题我们在前面也提到过，也很显而易见：「线性」回归分析，如果变量之间的相关性不是线性的，你就不能使用线性回归分析了。这个假设不需要额外地检验，在我们进行线性回归模型拟合的时候，采用了R2来判断拟合优度。如果R2接近0，说明我们的拟合并不好，也侧面说明我们的数据并不是线性相关。

线性回归要求必须线性相关

第二个要求是残差正态性，即残差的分布必须服从正态分布。需要注意的是，这里的正态分布要求不是数据本身，而是残差。如何得到残差？我们不需要进行计算，在使用lm( )函数的过程中，R就已经为我们计算好了残差，只要直接调用即可。检验正态分布的方法与之前提到的一样，使用Q-Q图或者shapiro.test( )函数都可以。我们以上一期的english数据为例，回顾一下建模过程。

# 加载languageR包library(languageR)
# 建立线性回归模型eng.m <- lm(RTlexdec ~ WrittenFrequency, data=english)
# QQ图检验正态分布qqnorm(eng.m$residuals)
# Shapiro-Wilk检验shapiro.test(eng.m$residuals)

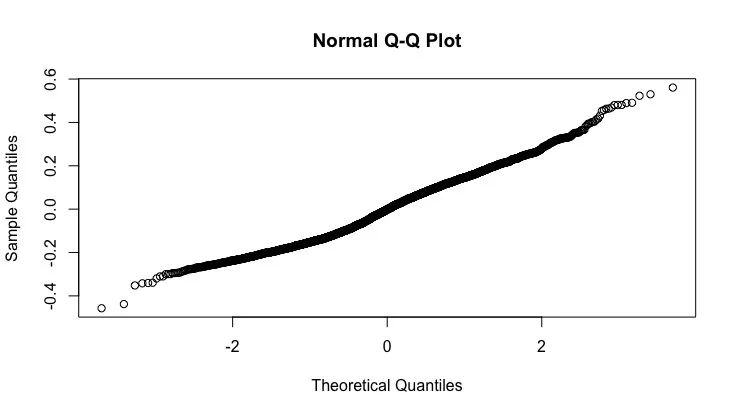
正态分布检验示意

最后是残差的方差齐性。可能很多人会疑问，我们的回归分析大部分一个自变量只对应一个因变量，怎么计算方差？要注意，我们这里提到的方差齐性，指的是「残差」而不是原始数据。如果以残差为纵坐标，自变量为横坐标绘制散点图，它的分散比较均匀，残差没有出现随着自变量的变化而变化，那么说明方差是齐性的。反之，则说明反差的方差不是齐性的。

残差的方差齐性

如何检验回归分析中残差的方差齐性？我们可以借用car包中的ncvTest( )函数或spreadLevelPlot( )函数进行检验，前者与shapiro.test( )函数一样，直接输出结果，如果出现显著性差异，则说明方差不是齐性的。后者则与Q-Q图一样会输出最佳拟合曲线的拟合值与残差绝对值的散点图，如果点没有均匀分布在水平线上下，则说明方差不是齐性的。我们以eng.m为例，那么如下：

# 加载car包library(car)
# 使用ncvTest函数检验方差齐性ncvTest(eng.m)# 使用spreadLevelPlot检验方差齐性spreadLevelPlot(eng.m)

通过检验结果可以看到，我们上次的数据并不具有方差齐性，因此我们需要考虑不能使用线性回归分析进行检验。

方差齐性检验

综上所述，在进行线性回归分析的时候，我们主要的步骤是：建立线性回归模型，查验模型是否符合三个前提假设；创建null model；对两个模型进行假设检验。

线性回归分析基本步骤

现在，我们了解了最基础的线性回归分析方法。但是显而易见的是，我们的语言研究中并不可能只有一个因素对因变量有影响，我们可以在有多个预测变量对情况下，对实验数据进行回归分析吗？答案是肯定的，这时候我们需要采用的方法叫做多元回归分析(multiple regression analysis)。

在面对多于一个预测变量的情况下，我们使用的方法被称作多元回归分析。它与简单的线性回归分析原理是一样的，不同之处在于，对于每一个额外的（多出来的）预测变量，我们都要赋予它们一个相关系数。那么，我们可以一直加需要的相关系数，那么我们的多元回归分析的基本公式则是Y = b₀+ b₁X₁+ b₂X₂+ ... + b_nX_n+ ε，每一个系数表示其对应的预测变量对因变量的影响，表现在图上就是斜率的大小。

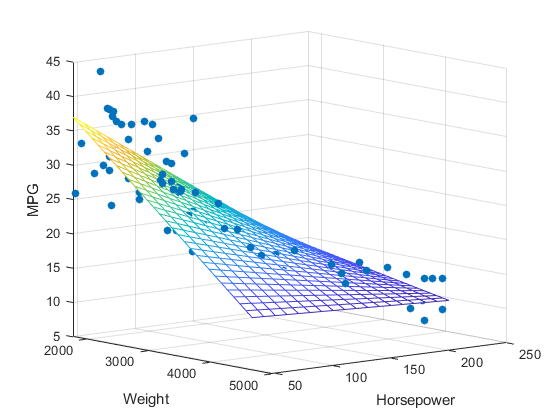
多元回归分析示意（两个预测变量）

多元回归分析所使用的函数依旧是lm( )函数，我们继续以languageR包中的english数据为例。上期我们考察了阅读时间RTlexdec和书写频率WrittenFrequency之间的关系，假设我们认为LengthInLetters这一列的数据对RTlexdec可能也有影响，那么我们就直接使用➕把这个因素加在后面即可，表示我要考虑该因素。为了进行比较，我们把null model、一个预测变量的模型、两个预测变量的模型如下展示。

eng.base <- lm(RTlexdec ~ 1, data=english)eng.m.1 <- lm(RTlexdec ~ WrittenFrequency, data=english)eng.m.2 <- lm(RTlexdec ~ WrittenFrequency + LengthInLetters, data=english)

进行拟合后，要记得查看拟合优度。这里我们假设拟合很不错，我们的下一步就是进行检验分析，查看预测变量对因变量是否有影响。我们分为自下而上(bottom-up)和自上而下(top-bottom)两种方式，前者是先将简单的拟合模型进行比较，慢慢加预测变量，而后者与之相反，率先从最复杂的模型开始。我们以自下而上的方式为例，首先比较eng.base和eng.m.1，出现了显著性差异，说明第一个预测变量WrittenFrequency对RTlexdec有显著影响。接着我们继续加一个预测变量，比较eng.m.1和eng.m.2，发现并没有出现显著性差异，这说明第二个预测变量对因变量没有出现影响。我们也可以直接把它们放在一起，即anova(eng.base, eng.m.1, eng.m.1)也是可以的。

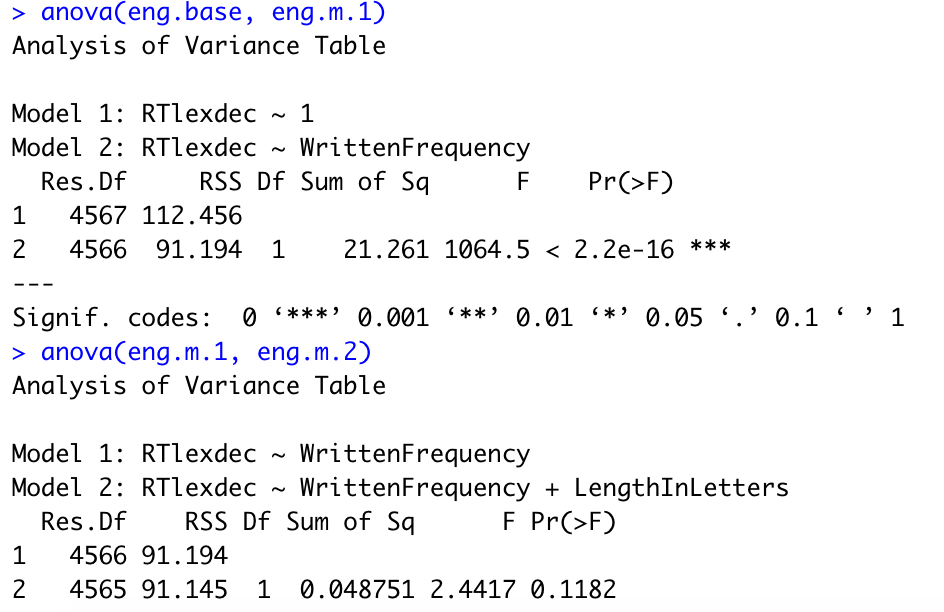
多元回归的分析检验

最后，我们需要指出，既然出现了多个变量，那么我们就要考虑主效应和交互效应的问题。如何把两个预测变量的交互效应考虑进多元回归分析中？以english为例，我们可以这样进行建模。

eng.m.3 <- lm(RTlexdec ~ WrittenFrequency +               LengthInLetters +               WrittenFrequency : LengthInLetters,               data = english)

其中的WrittenFrequency : LengthInLetters意味着我们考察的是它们的交互效应。建立好模型后，继续使用anova( )分析结果，有没有显著性差异呢？这里就留待你自己运行代码查看了。

之前我们谈到的所有预测变量，全部是连续型预测变量，而有一些研究涉及到的是分类型变量。比如，动词词组或名词词组这样的短语类型对阅读时长的影响，这时候我们的预测变量则变成了分类型，还可以继续使用回归分析吗？如果输出结果是分类型变量，也可以回归分析吗？答案是可以。这一期讲了很多，所以这些问题留待下一期进行详细解释。