1. 估计和假设检验可以实现推论性统计。

2. z分数将数据标准化，可以描述数据中个体距离平均值的距离。

3. 分布分为正态分布和偏态分布，偏态分布进一步分为正偏态和负偏态。

4. 检测数据分布是不是正态分布有多种办法，包括计算峰度和偏度，使用分位图，使用Shapiro-Wilk检验或K-S检验。

R: The R Project for Statistical Computing

https://www.r-project.org/

RStudio:

https://rstudio.com/

研究者通常不可能观察或检验总体中的每一个个体，而是选择采集样本数据对总体进行推论，这是我们之前一直提到的推论统计过程。在推论过程中，最常用且最普遍的方法是假设检验(hypothesis testing)。下面我们将详细介绍假设检验，为我们以后的统计分析打下基础。

假设检验是一种统计方法，它使用样本数据评估关于总体参数的假设。换句话说，在研究过程中，我们首先根据总体做一个“预期”，然后通过样本数据的结果来评判这个预期是真是假。一般假设检验遵循以下步骤：

1. 陈述零假设和备择假设。

2. 选择显著性水平。

3. 确定统计检验方法。

4. 收集样本数据并计算统计量。

5. 计算拒绝域。

6. 作出统计推断（拒绝或接受零假设）

下面，我们对步骤中的一些术语进行详细解释。

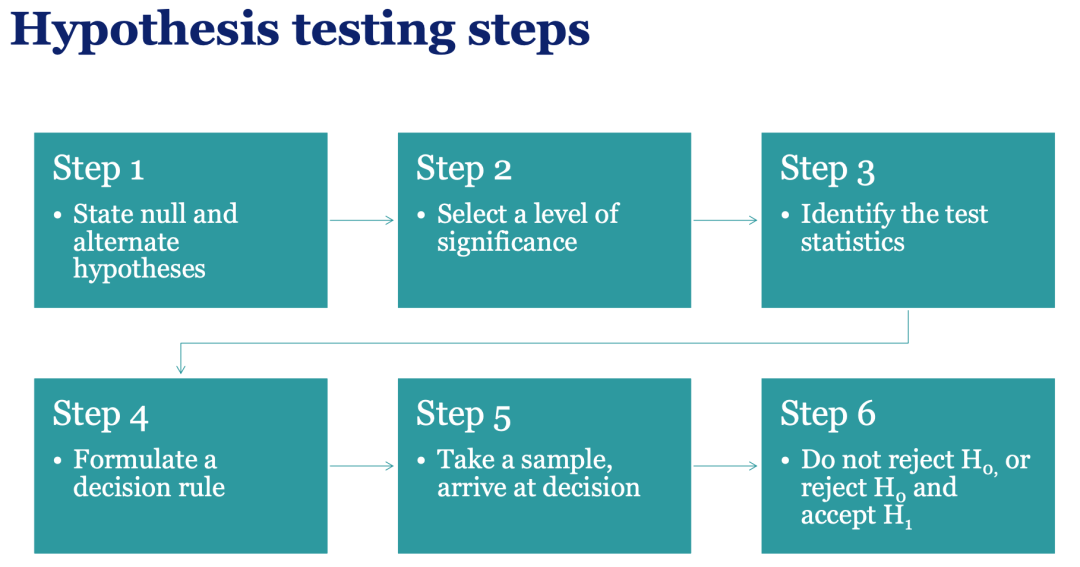
假设检验的一般步骤

假设检验的过程始于陈述假设。在陈述时，我们需要说明两个相反的假设，其中最初和最重要的那个假设被称为零假设(null hypothesis，又称虚无假设，记作H₀，其中的H代表hypothesis），它代表自变量对因变量没有影响，即不存在改变，没有差异，什么也没发生。另一种假设与零假设相反，称为备择假设(alternate hypothesis，又称对立假设，记作H₁)，它代表自变量对因变量有影响。比如，我们考察焦点对语调中音高的影响，那么我们可以做如下的假设：

H0：焦点对音高没有影响

H1：焦点对音高有影响

这是我们对假设的描述，实际上我们比对的是在焦点影响下的音高和没有焦点的音高是不是有数据上的差异，这样我们就把“现象比较”转化为“数据比较”了。需要注意的是，H1只是陈述存在一些改变，但是并没有说明改变的方向是什么（比如升高或降低）。在特定研究中我们是可以设定改变方向的，这样就成为了方向性假设检验，之后我们会提到这个内容。

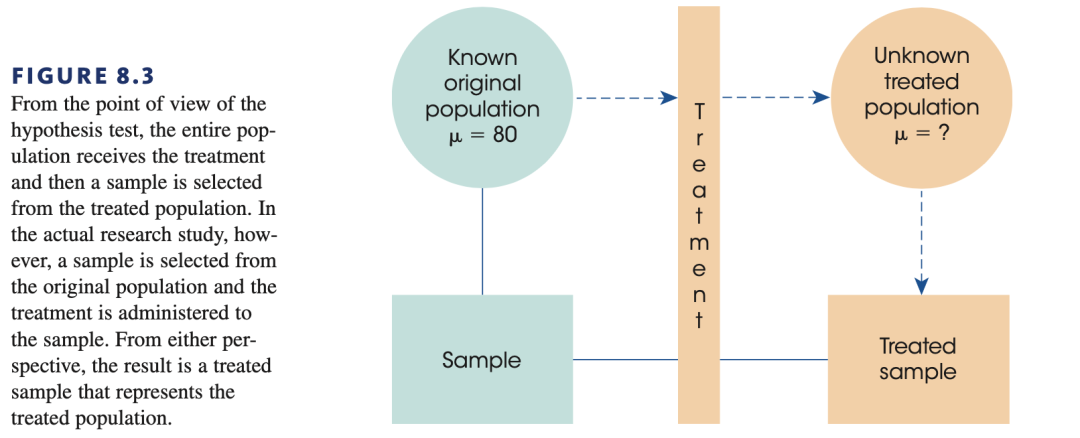
假设检验角度看的研究情况

假设检验的第二步是选择显著性水平(significance level)。显著性水平是一个概率值，它被用于定义在零假设是正确的情况下非常不可能出现的样本结果。举个例子，假设你是有名的枪手，平均成绩是7环。我该如何检验你这话是真是假？首先，我们会选择相信你，即“你的平均成绩为7环”（零假设，即实验将要采集的样本与你所说的情况没有差异），然后我开始让你开始发射并计算中的环数。如果你打了20发，平均值在6.7，那么足够说明你说的是真话，因为不可能每次都正好是7，在允许范围内浮动都说明你说的是真话。但是，如果你20次的实验中多次2环甚至1环，平均值已经低到2.8，那么我足够怀疑你说的是假话，因为对于一个平均7环的选手来讲，再怎么失误频频打到2环的概率是非常低的。所以这时候我们会选择拒绝零假设，认为你在说谎。

上面的例子就是我们所说的显著性水平。它是一个非常小的值，代表着“最不可能出现的情况”的概率。我们最常用的显著性水平是α=.05 (5%)、α=.01 (1%)和α=.001(0.1%)，这个也就是我们所说的p值。使用显著性水平来确定要不要质疑处理效应的原因在于，统计学中小概率事件在非常少的情况下才会发生，如果一旦发生了，说明我们一开始做的假设是有问题的，需要拒绝他。回到刚刚的例子，对于平均7环的人而言，能20发打出2.8环的成绩根本就是非常非常小概率的事件，或者说很不可能发生的事情。既然它发生了，说明你在说谎。

也因此，我们结合正态分布曲线，可以得到一片区域，这片区域代表着小概率事件发生的区域。如果数据落在这里，说明“很不可能发生的”小概率事件发生了，那么我们一开始的假设就是错误的，需要质疑/拒绝他。这一片区域也就是我们所说的拒绝域(rejection region)，又叫临界区域(critical region)。

拒绝域/临界区域图示

综上，我们把假设检验步骤中的重要概念进行了解读。之后的大部分统计分析方法，都遵循这样的检验步骤，我想你应该也能明白为什么p小于.05就要拒绝了。接着就是选择相应的统计分析方法，进行分析了。

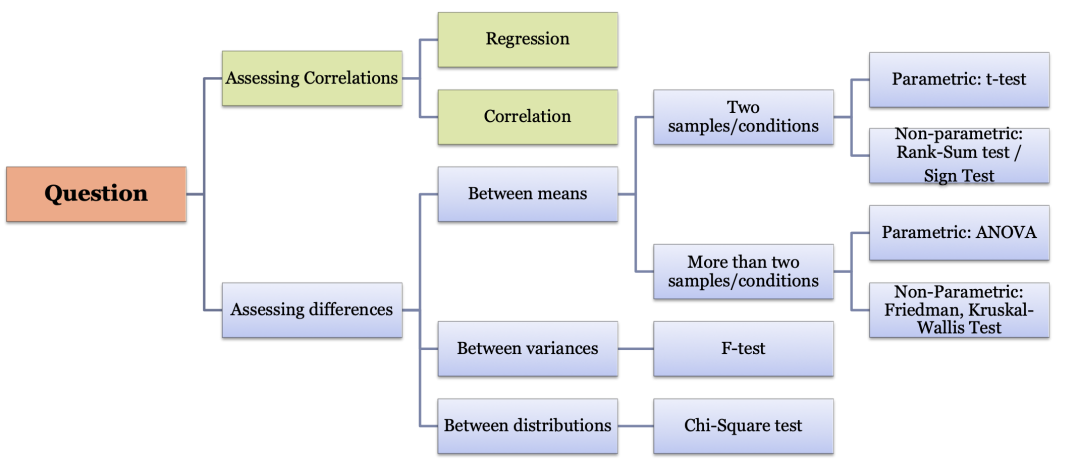
统计分析方法的选择

俗话说“常在河边走，哪有不湿鞋”，假设检验尽管帮我们做出了有关总体的一般性结论，但是有可能存在做出错误结论的可能，这种错误我们分别称作第一类错误(Type I error)和第二类错误(Type II error)。我们首先以形象的图示来表达这两类错误分别是什么。

莱顿大学Statistics in Linguistics课程讲义

第一类错误指的是当你得出了研究结果存在处理效应，拒绝了H0，但实际上它其实并没有处理效应（应该接受H0），这时犯的错误就是第一类错误。比如工厂生产了100个玩具，其中有5个次品。我们假设次品率是5%，只要我抽中的次品率低于这个数值就足够拒绝H0。然而就是欧气满满一次性抽样就抽中了这五个次品，这时我们怀疑你的次品率实际上超过了5%。此刻我们就犯了第一类错误。也就是说，我们对你进行采样的时候，样本是由极端值构成的，这就导致我们犯了第一类错误。那么犯这类错误的概率是多少呢？前面的显著性水平能告诉我们答案。具体来说，显著性水平确定了当H0为真的情况下得到样本在拒绝域的概率（即样本是由极端值构成的概率），因此，它定义了第一类错误的概率或风险，记作α。

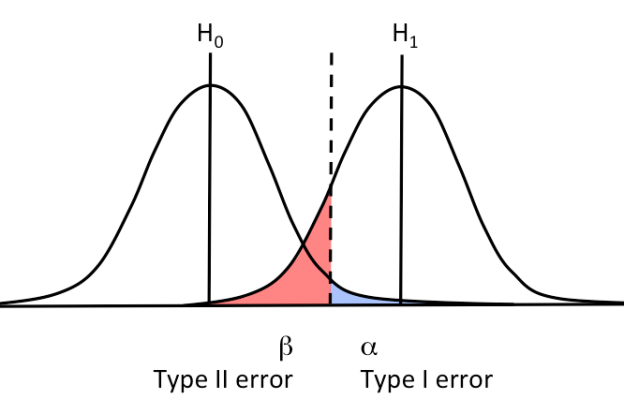
两类错误示意图

第二类错误与第一类误差相反，当处理效应真的存在的时候，假设检验没有检测到它，研究者做出了“接受H0”的结论，这种情况往往发生在处理效应比较小的时候。第二类错误的概率记作β，因为第二类错误是多种因素决定的，因此它是一个函数，而不是一个具体的数值。再拿上面的例子举例。假设100个玩具里面有10个次品，次品率已经到了10%，我们的假设是次品率为5%。这时我们抽了多次，恰好这次品全被躲过去，我们判定次品率低于5%。这时我们就犯了第二类错误，即明明数据有差异，但是我们没有检测到，选择了接受H0。

两类错误概率示意

那么我该如何避免这两类错误？可惜的是，这两类错误不能同时避免，减少一类错误发生的概率就会增加另一类错误的概率。我们再回到下面的这个示意图。可以看到，我们的样本由极端值构成，导致我们对数据进行了错误的推断，虚线位置就是显著性水平。为了减少第一类错误，我们可以选择变更显著性水平，比如我采用了更小的α=.001，这时候虚线往右移，确实蓝色区域（第一类错误的概率）减少了，但是红色区域（第二类错误的概率）却在增加。因此，不可能完全规避两类错误。但我们不难看出，第一类错误的风险更大，因为它会导致错误的研究报告，因此规避第一类错误是最好的选择，同时它的影响因素也很单一，完全由研究者控制在假设检验中，所以我们通常会选择不同的α水平来规避第一类错误的风险。

两类错误示意图

上面我们提到过，绝大多数情况下我们所做的假设检验是不带有方向的，即只说明自变量对因变量有处理效应存在，但并不说明自变量会对因变量造成什么样的影响。这种情况下，我们所设计的是一种双尾检验(two-tailed test)，换句话说，我们的拒绝域在分布的两端，这也是我们通常使用的研究格式。除此之外，还有单尾检验(one-tailed test)，这类检验的拒绝域往往位于一端，其假设具有方向性。比如，我做的假设不是“焦点对音高有影响”，而是“焦点会提高基频曲线”，这时的假设就是带有方向性的假设，我们做的检验也就变成了单尾检验。

单尾检验和双尾检验示意图

单尾检验和双尾检验的差别主要在于他们拒绝H0的标准。单尾检验允许你在样本和总体之间的差异较小时拒绝H0，然而这个差异同时也被规定好了方向（增加或减少）。而双尾检验则不依赖方向，只要出现了变化/差异我都可以拒绝H0，但是它需要相对较大的差异才能拒绝，也因此很多研究者更倾向于双尾检验，因为它需要更多的证据（样本和数据）来达到双尾检验的要求。

那么我该如何选择呢？当你的实验没有强烈的方向性，或者你觉得两个效应（增加或减少）相反时，比如一个增加一个减少，采用双尾检验会更好。如果你的研究有方向性，那么使用单尾检验更佳。需要注意的是，如果你采用了双尾检验不能得到显著结果时，万万不可再用单尾检验补救。

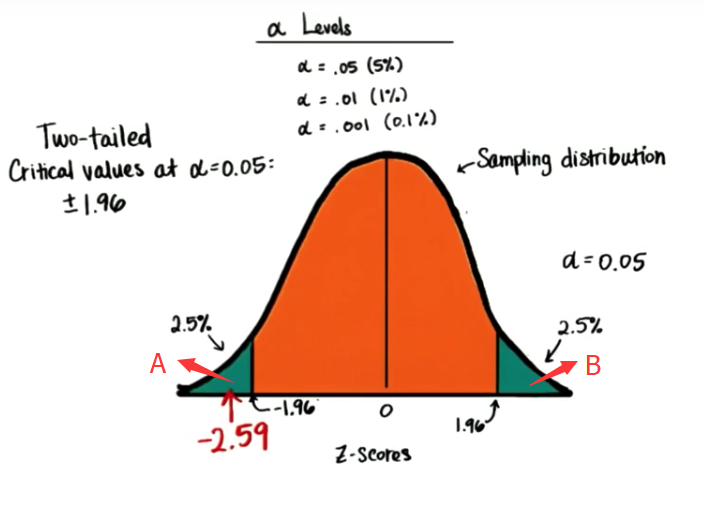
双尾检验需要更多的样本差异来支撑

至此，我们对假设检验进行了概述。下一期我们将正式开始统计分析的步骤以及如何在R中实现统计分析。

—END—

排版：Xu & Yang