元分析的一大优势（也是元分析可以在实际研究中提供帮助的原因之一）就是，它允许合并更多数据来获得更精确的汇总效果。然而即使在元分析中，缺乏统计功效仍是个问题。尤其是在临床领域，通常只有很少的研究可用于综合。例如，Cochrane Database里系统综述纳入的研究中位数为6（Borenstein等，2011）。统计功效的问题会更严重，一旦我们考虑到（1）许多元分析研究者还希望执行亚组分析和元回归（需要更高的统计功效），（2）许多元分析具有很高的异质性，这就降低了精准性，从而统计功效也降低了。

功效直接与II型错误水平(β)有关，定义Power=1-β。常规操作是设置I型错误水平（α）为0.05，假设I型错误严重性是II型错误的四倍（即犯假阳性错误严重性是假阴性错误的四倍）。因此，将β设置为0.20，则统计功效power=1- β=1-0.20=0.80。

那么在元分析中我们应该做什么样的假设呢？

尽管开展基础研究的研究人员可以根据他们想要发现的效应大小来计划样本量大小，但元分析的情况有所不同，我们只能使用已经存在的材料。但是，我们可以控制要纳入元分析的研究数量（例如，通过设定更宽松或更严格的纳入标准）。因此，我们可以通过在元分析中纳入或多或少的研究来在一定程度上改变我们的统计功效。在事先计算元分析的功效时（先验功效），我们需要考虑以下四件事的有关假设。

1.已经纳入或者可以纳入的k值

2.想要纳入的研究的整体规模（该领域的研究通常较小还是较大？）

3.想要确定的效应量大小。这一点尤为重要，因为我们必须假设效应值必须多大才具有临床意义。一项研究计算得出，对于抑郁症的干预措施，即使效应值小至SMD=0.24，对于患者可能仍然有意义（Cuijpers等，2014）。如果我们要研究干预措施的负面影响（例如死亡或症状恶化），则即使很小的效应量也非常重要，应予以检测。

4.研究的效应量的异质性。因为这也会影响元分析的准确性，因此也影响发现显著效应的可能性。

除了这些参数，其他分析也很重要，比如亚组分析。每一个亚组里有多少个研究，我们希望在亚组找到多大的效应量？如果我们假设某种干预对于某些患者无效，这一点尤其重要，因为我们不想发现没有效应只是因为功效不够。

后验的统计功效（post-hoc power tests）：功效滥用

请注意，功效分析应始终进行先验，即在开展元分析之前。

在分析开始之后进行的功效分析（“后验”）从根本上是有缺陷的（Hoenig和Heisey，2001年），因为它们涉及到“功效实现悖论”（power approach paradox），在这种情况下，一项没有发现显著效应的分析被认为可以提供更多的证据证明，当p值较小时，原假设为真，因此，发现真效应的检测力是比较高的。

16.1 固定效应模型 fixed-effect model

在固定效应模型下确定元分析的功效，我们必须在备选假设正确时（即在有效应时）假设分布的真实值。对于常规研究中的功效分析，服从Z分布。根据 Borenstein等（Borenstein et al。2011），我们称λ为真值来明确表示我们正在进行元分析，而不是主要研究。

λ 的定义为： 

      其中是真实的效应值，是其方差，可以用固定效应模型的公式计算：

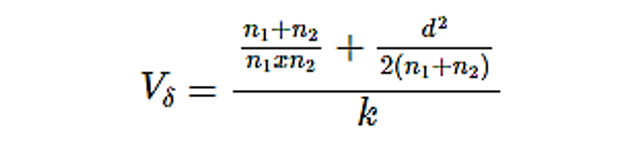
其中k是所有纳入的研究数量，n1和n2是我们在研究中假设的每个试验组的平均样本量。假定正态分布以及使用λ，我们可以计算功效值：

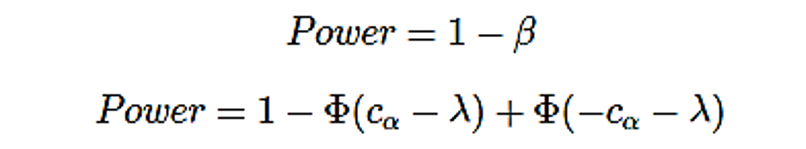
其中是Z一个的临界值, Φ是标准的正态密度函数，我们需使用以下公式计算功效：

幸运地是，我们不需考虑太多关于上述统计细节的事，因为我们有“power.analysis”功能，它可以轻松地进行固定效应模型下的功效分析。这个功能是dmetar 包的一部分，如果你已经安装好这个包，可以轻松地调用：

      library(dmetar)

如果你不想用dmetar包，你可以找到源代码，通过完整地复制粘贴来实现。需要用ggplot2包来画图。这个功能，涉及以下参数（及参数说明）：

d：与对照组相比，治疗/干预组的假定的或合理的总体效应值大小，以标准化平均差（SMD）表示。效应值大小必须为正数值（即表示为正效应大小）。

OR:与对照组相比，治疗/干预组的假定的或合理的总体效应值大小，以优势比（OR）表示。如果同时指定了d和OR，则仅针对d值计算结果。

k：预期的纳入元分析的研究数量。

n1：纳入元分析的研究中干预组的预期或合理的平均样本量。

n2：纳入元分析的研究中对照组的预期或合理的平均样本量。

p：用于功效计算的Alpha水平。默认值为alpha = 0.05

heterogeneity：异质性，元分析假设的研究间异质性水平。可以是“fixed”（表示没有异质性）/固定效应模型，“low”（表示低异质性），“moderate”（表示中等大小的异质性）或“high”（表示高异质性）。默认值为“fixed”。

现在，举一个例子。假设d=0.30对于我的元分析领域来说是可能的以及有意义的。还假设所分析的研究平均样本规模都很小，每个试验组中有25名参与者，并且分析中将有10项研究。按照惯例，将α水平设置为0.05。

那么相应的代码是：

power.analysis (d=0.30,
k=10,n1=25,n2=25,p=0.05)

该功能的输出为：

## Fixed-effect model used. 

## Power:## [1] 0.9155008

从上图可以看到，如果假定d=0.30，很快就达到了足够的功效（虚线所示），即使只包括很少数量的研究。但是如果假定较小的效应值，如d=0.10，即使有50项研究也不足以找到真正的效应。

16.2 随机效应模型Random-Effects Model

随机效应模型的统计功效，由于所抽样的总体来自不同的群体，所以计算真均值效应的方差公式会稍微有些不同, 即考虑了研究间异质性进而纳入了τ²，具体公式如下所示：

Vδ^∗=(V_Y+τ²)/k

不过由于我们无法事先了解研究间的异质性，所以我们面临这个值如何设定的问题。Hedges和Pigott（2004）提出用下面的三个公式解决研究间异质性不同程度的困境，较小的异质性可采用公式2，中等程度的异质性可以公式3，高异质性可采用公式4。

Vδ^∗=1.33×(V_Y/k)                        -------------公式2

Vδ^∗=1.67×(V_Y/k)                        -------------公式3

Vδ^∗=2×(V_Y/k)                             -------------公式4

这些计算过程不用担心，可以用R里的power.analysis函数完成。和固定效应模型的统计功效分析所用参数一样，只不过这次需要在函数里指明异质性程度，如下面的分析代码里研究间的异质性程度为中等程度。注：通常随机效应模型的统计功效分析默认选择中等异质性程度。

power.analysis (d=0.30, k=10,n1=25,n2=25,p=0.05,heterogeneity = "moderate")

我们可以看到结果显示该示例计算出的统计功效为73%，小于固定效应模型中计算出的91%的统计功效。当统计功效低于80%时意味着将无法有效检验出效应量0.30在统计上显著的结果。此外与固定效应模型结果的差异，与较大的异质性有关。异质性增加会降低对效应值估计的精确性，因此很需要统计功效。具体关系如下图所示，横坐标为研究的数量，纵坐标为统计功效，d为效应量。

图16.1 随机效应模型的统计功效。

同组线图中颜色加深表示研究间的异质性更高

16.3 亚组分析Subgroup Analyses

通常，当在元分析中进行亚组差异检验时，我们可能会感兴趣的是，鉴于手头的数据材料，两个亚组之间需要多大的效应大小差异才能使差异变得显著。为了评估这一点，对亚组差异进行功效分析可能会有所帮助。

我们创建了一个名为power.analysis.subgroup的函数，通过Hedges和Pigott(2001)描述的公式来计算亚组差异检验的功效(只使用两个亚组)。这个函数是dmetar软件包的一部分。如果你已经安装了这个包，你必须先把它加载到你的库中。

假设我们有一个亚组分析，其中亚组1的集合效应大小为g=0.30，标准误差为0.13，亚组2的效应大小为g=0.66，标准误差为  0.14 . 我们就可以使用这样的函数：

从输出中，我们可以看到，我们的分组测试的功效（47%）是不够的。还可以看到，在其他参数不变的情况下，效果大小差异至少要达到0.536，才能达到足够功效。

16.4 功效计算工具

如果您感到懒惰，或者想在不同的假设下快速检查元分析的功效，那么你可能需要一个工具来使你更轻松地计算功效而无需运行R。

因此，我们构建了一个在线功率计算器工具Power Calculator for Meta-Analysis (https://mathiasharrer.shinyapps.io/power_calculator_meta_analysis/)。这些计算都是基于我们在前面各章中描述的公式和函数。

具体操作而言，你需要通过设置各个功效分析（power analysis）的参数而得到对应的功效结果。如上图所示，你需要设置效应值（effect size, SMD），假设为两亚组情况下的各亚组的样本量，纳入研究的数量（k），适配的分析模型，以及预期的p值。

由上图设定的各项参数值，我们可以得到最终的功效值为92.9%。