3. Density plots

还是同样使用 iris 数据。

在数据分析时，如果我们要查看定量变量 (quantitative variable)或者连续变量 (continuous variable)的分布时，直方图通常是首先。但是，以上周更新中我们所得到的直方图来看，当变量分布不均匀时，整个直方图就会呈现出较大的波动。而同样能看查看变量分布但又能消除这种波动的分析方式就是 Density plots（密度图）。

在Jamovi里使用密度图的方法有两种。

-- 第一种就是按照基本的流程，先选定变量，再取消statistics下的所有默认选项，再找到密度图，得到分析结果。

-- 第二种方法更加便捷，就是在我们之前所得到的直方图的基础上直接创建密度图。

首先打开之前保存好的直方图的数据，单击第一个直方图，左侧会出现操作区，找到密度图的选项，就能在直方图的基础上生成密度图，这也是为什么密度图的选项在直方图大类下面。

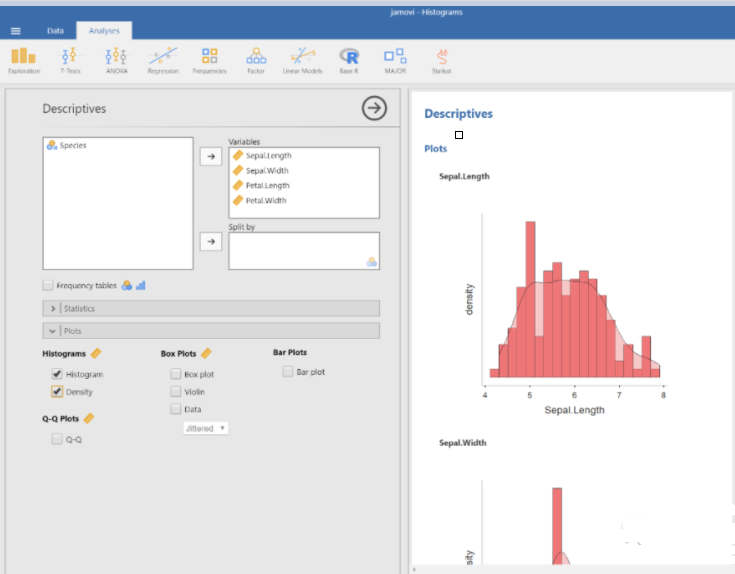
这时可以看到，密度图缓和了直方图原有的波动，更为平滑。密度图的整个形状并没有百分百还原直方图的比例，因为它对变量进行了均值的计算，但它呈现的是相同的整体趋势。如果只想要密度图而不需要直方图的话，可以取消选定直方图，只保留密度图，则可以得到下面的结果。

这里可以看到，当只有密度图时，整个密度图表现出来的分布趋势没有变化，但是比例有所调整，更加明显了。

直方图分析中，以种类为细分的标准所得到的每个变量的分析结果也可以通过密度图来呈现。

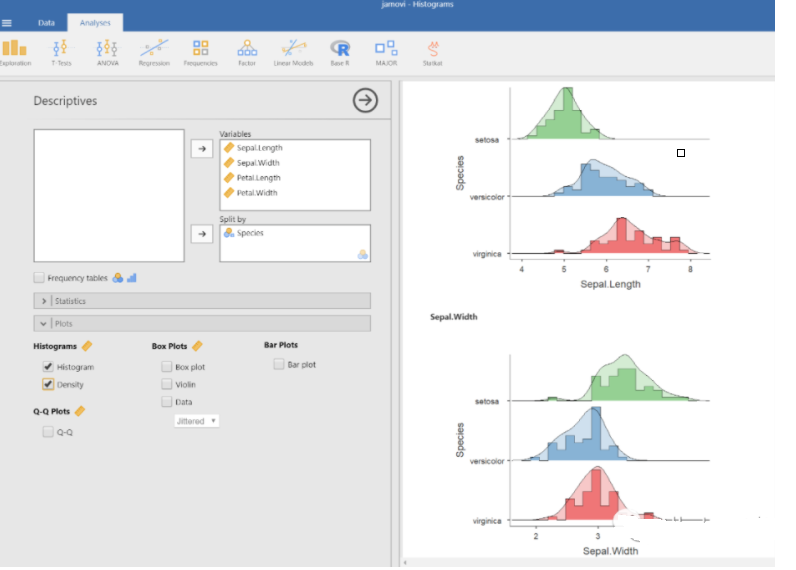
              (密度图和直方图一起呈现)

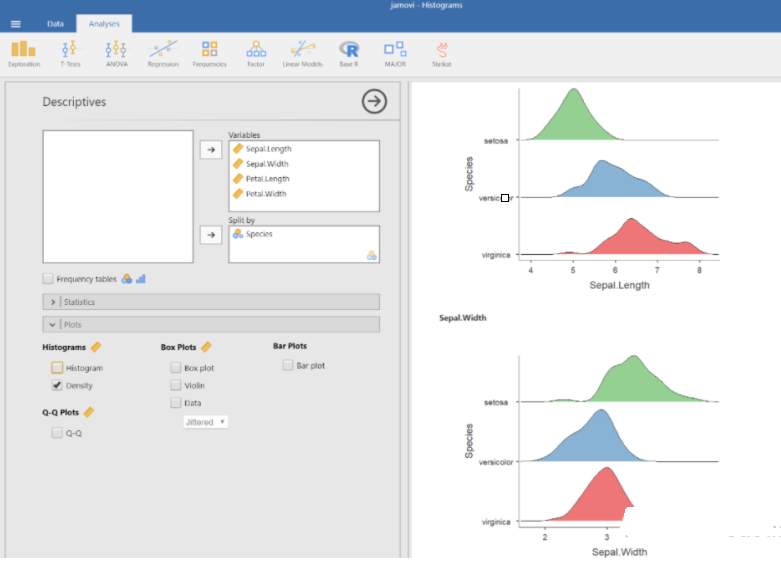
               (密度图单独呈现)

在上面这个单独呈现的密度图里，我们能清楚地看到每一个数据堆的形状都暗示了它处于单峰分布 (unimodal distribution)的状态，有一个明显的峰值，且每一个峰值处于不同的位置。

总体来说，密度图相对于直方图的优点在于，它更加清楚地展现出了变量分布的整体趋势，更加平滑，让人在看的时候不会因为直方图的锯齿形状而分心，更加简洁明了。

4. Box plots（箱形图）

再来看箱形图。同样，这里也是使用Iris数据。

在做数据分析时，离群值 (outliers)可能是个非常严重的问题，因为离群值可能会使原本的分析和结论都不成立。 因此，当数据中存在异常值时，我们要特别注意，而最简单的找出离群值的方法并不是使用直方图或密度图，而是使用箱形图。

还是类似的操作，在密度图的基础上，生成箱形图。但是，从下面的图里可以看到，箱形图属于Box plots大类，和密度图不在一起，因此当我们选择箱形图的时候，箱形图并不会在密度图的基础上一起出现，而是单独出现。这时，取消密度图的选定，就能得到单独的箱形图。

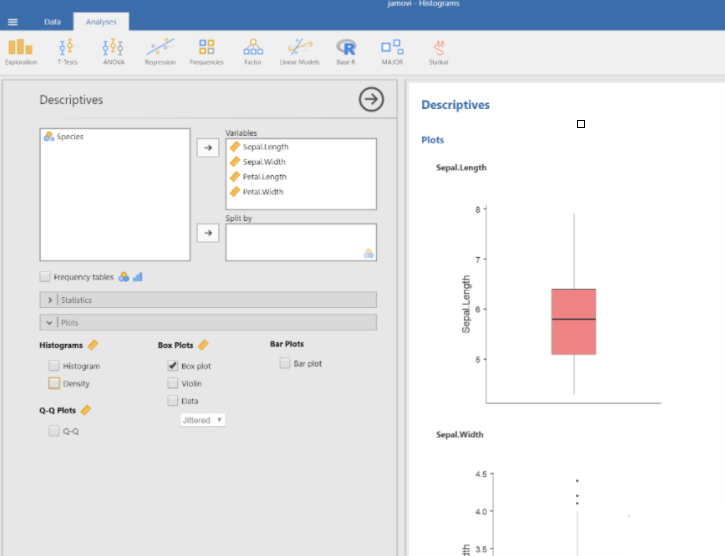
在箱形图中，离群值以单个的点的形式出现。

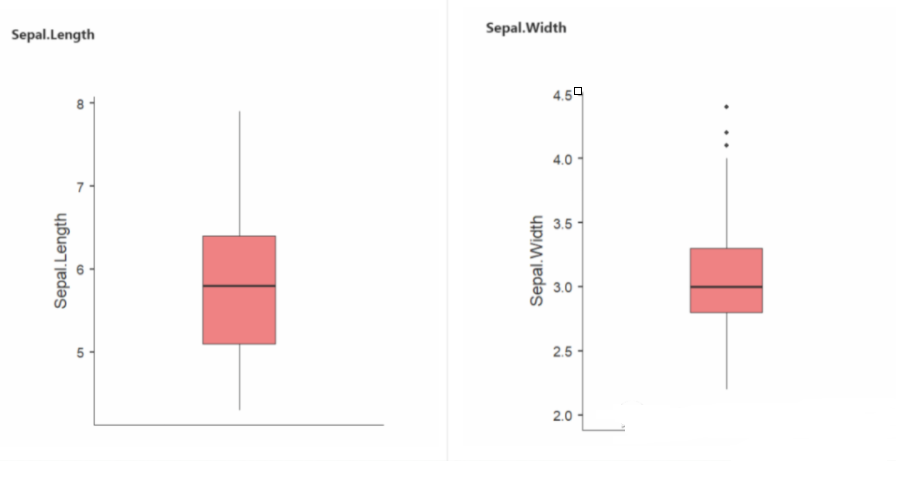
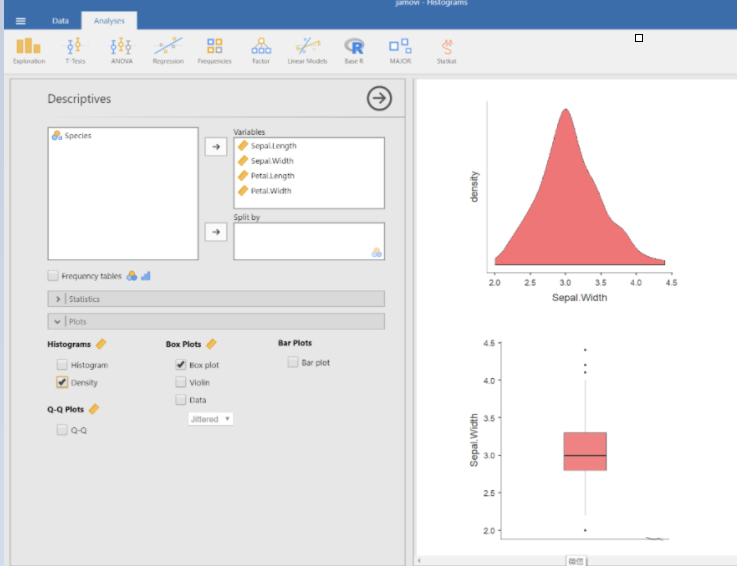
从花萼的长度(左)和花萼的宽度(右)的对比可以看出，花萼长度中没有离群值，而花萼宽度中有离群值。

花萼宽度中有离群值的原因在于变量分布的形态本身。

从密度图上可知，这是一个 leptokurtic distribution (高狭峰分布)，可以简单理解为和常态的分布曲线相比，中间部分更加细长。而高狭峰分布本身就意味着会有很多离群值。

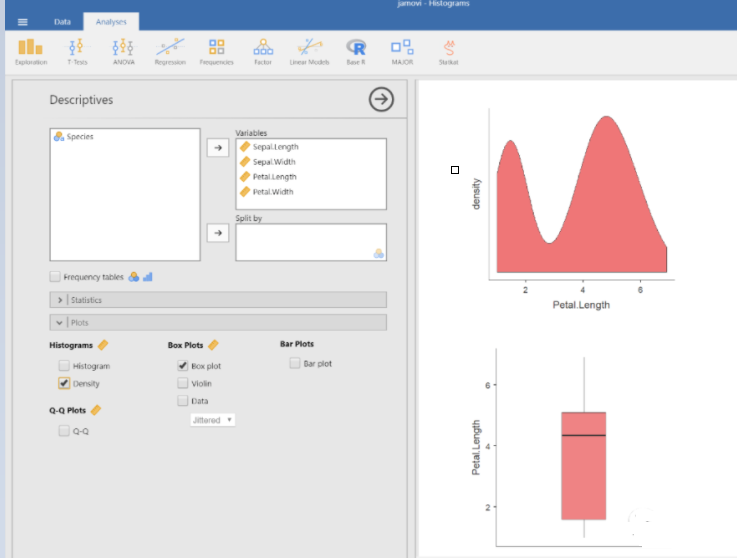
对花瓣长度来说，它没有离群值。这也是由其本身的分布状态决定的。

从密度图可知，花瓣长度的分布状态呈现出的是双峰分布的形态。由于双峰分布本身的特性，箱形图的中间部分分布很广，因此没有什么离群值。

同样，以品种分类后的对比图也可以用箱形图来分析。

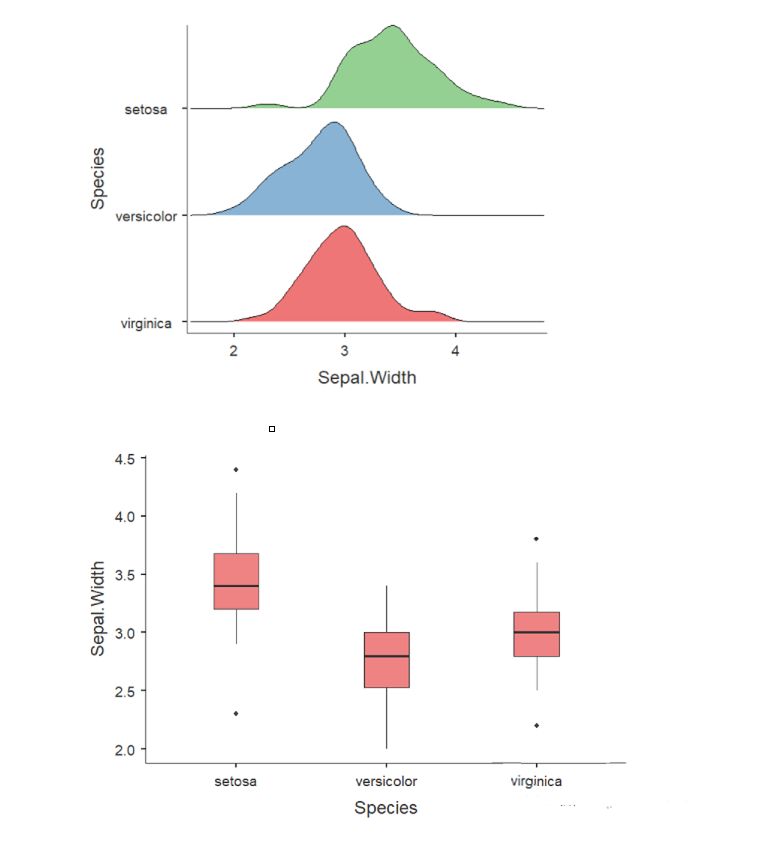
也是先来看花萼长度的对比图，这里可以看到三种鸢尾花中，只有virginica有一个离群值，在下方。

在花萼宽度中，setosa 和 virginica各有两个离群值，分别以对称的状态分布在上方和下方，整体看起来也还不错。

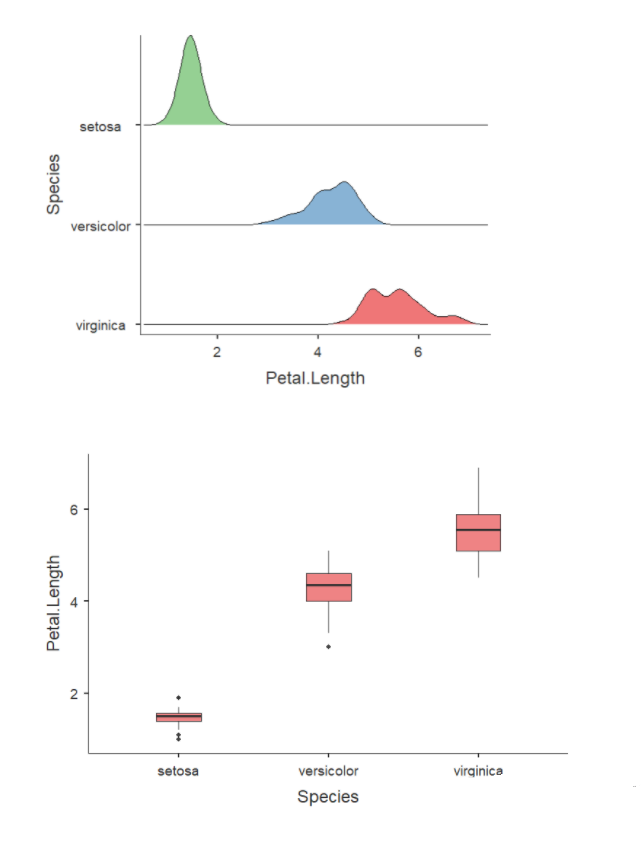
在花瓣长度的箱形图里可以看到，setosa这个种类的花瓣长度的分布呈现出一种被压扁了的状态，同时它的分布范围非常狭窄，与其他两组相距甚远，并且有好几个离群值。对比上方的密度图可以发现，setosa的花瓣长度的密度图本身也是高狭峰分布的状态，很容易有离群值。

而最后的花瓣宽度也是类似的结果：

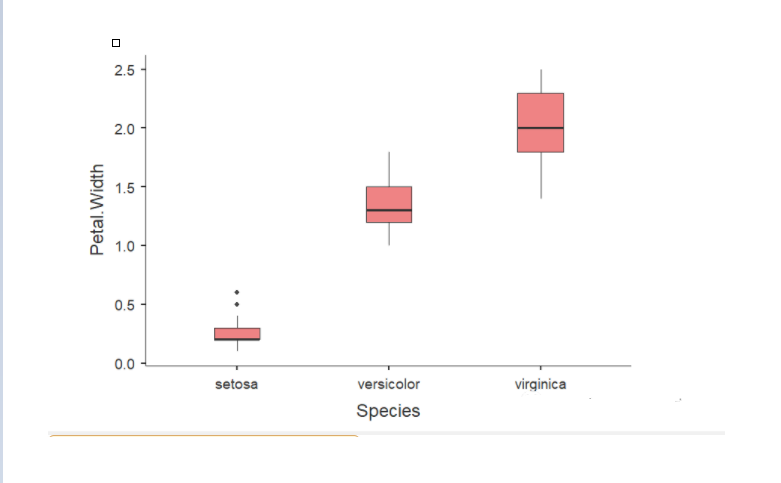
简单的总结：

箱形图可以帮助我们找到数据中的离群值。从上面的结果来看，Iris这个数据本身没有太多的离群值。我们可以从上面的数据中知道，以上三种类型的鸢尾花在花萼和花瓣的长宽度上各有不同，而箱形图也很好地展现出了这一部分的信息。同时，箱形图还让我们能够进一步地检测数据中的离群值对整体数据所有的潜在的影响。

原本计划将剩下的部分全部更新完，但是太长了，这次只更新密度图和箱形图的部分，剩下的内容，我们下期再见。

希望对你有所帮助 :)

欢迎讨论~