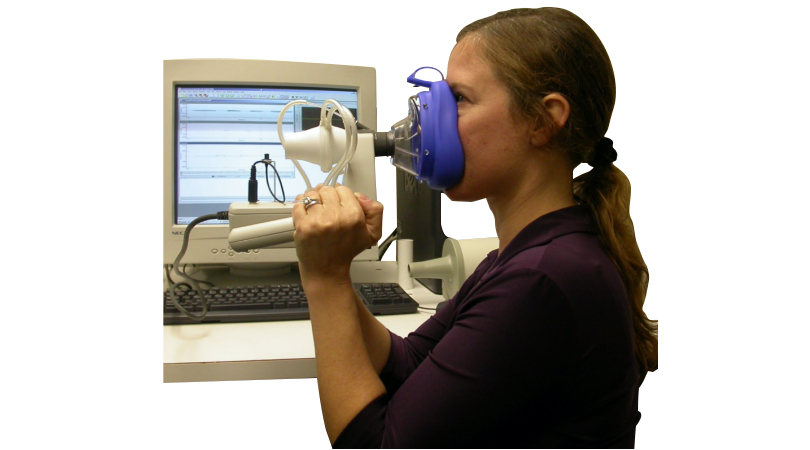
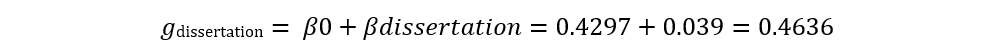【元分析的多水平本质 The multilevel of Meta-analysis】本章讨论“多层”元分析中合并效应量(pooling effect sizes)问题,其实,元分析的本质就是多层性的,回看4.2章中讨论的随机效应模型的公式:我们假定了随机效应模型中存在两个变异源(variability),一个是组内方差(取样误差ϵk),另一个是组间方差(研究间效应量存在的差异ζk),随机效应模型的目的是估计真实效应量θk分布的平均值,μ。这两种变异源对应元分析数据中的两个层次:“被调研者”层面(level 1)和“研究”层面(level 2),如果分解该公式的话,可以对应拆解到两个层面:
可见,元分析模型本身已经具有“内置”的多层属性,其实固定效应模型也可以看成多层结构,即level 2层面的ζk设为0。
【三层元分析模型Three-levelmeta-analytic models】元分析具有多层次的结构。这使我们能够进一步扩展此结构,以更好地反映我们的数据。三层模型(Cheung, 2014; Assink & Wibbelink, 2016)是实现这一目标的好方法。统计独立性是元分析的核心假设之一(Hedges, 2009)。如果效应大小之间存在依赖性(即,效应大小相关),则可能人为地减少异质性,从而导致假阳性结果。依赖可能来自不同的来源(Cheung, 2014):- 个体研究者引入的依赖性。例如,进行这项研究的科学家可能已经从多个地点收集了数据,或者可能将多个干预措施与一个对照组进行了比较,或者他们可能使用了不同的问卷来衡量感兴趣的结果(例如,他们也使用了BDI和PHQ-9评估患者的抑郁症)。对于所有这些情况,我们可以假定在报告的数据中引入了某种依赖性。
- 元分析者自己介绍的依赖性。例如,一项元分析可以侧重于特定的心理机制,并包括在不同的文化领域和世界中进行的研究。当在相同文化背景下进行研究时,所报告的结果更为相似似乎是合理的。
我们可以通过将第三层集成到我们的元分析模型的结构中来解决这种依赖性。例如,可以模拟不同的调查表嵌套在研究中。或者可以创建一种模型,其中将研究嵌套在文化区域内。如下图所示,这将创建一个三级的元分析模型。
Metafor软件包特别适合于在元分析中拟合各种三级模型。在建立元分析模型时,我们以前主要使用过meta函数,因为我们认为此程序包的代码在技术上稍差一些。但是,一旦正确准备了数据,metafor也将非常容易使用。我们将在下一章中进行介绍。12.1 三水平的模型拟合Fitting a three-level model
12.1.1 数据准备
在开始拟合模型之前,我们需要加载metafor包:本章将使用mlm.data数据集。它为metafor进行模型拟合做好了准备。让我们来看一下这个数据集:这个数据集有80行5列(即包含5个变量)。前四个是最重要的:
ID_1和ID_2。在这两列中,我们存储了多层模型中不同层次的单个效应值和集群的标识符。并将这些列保留为通用列以容纳各种类型的数据结构。例如,我们可以想象一个场景:ID_2对应于我们在一项研究中发现的不同的效应值(例如,不同抑郁测量的不同效应值)。在此例中,ID_2中的效应值将嵌套在ID_1(研究)中定义的较大簇中。还有一个例子是,ID_2实际上象征着单个研究的唯一标识符,然后这些研究嵌套在ID_1所示的更大的集群(例如,文化区域)中。y和v。这两列储存了关于效应值的数据。格式类似于meta中的metagen函数。列y包含效应值(d、g、r、z或其他连续效应值的度量)。v列包含样本方差,可以通过对标准误差进行平方来获得。有另外的两列包含亚组分析所需的数据。然而,要使用metafor进行亚组分析,我们需要存储的数据与第7章中的数据稍有不同。这次,我们不使用包含亚组级别的因子向量作为字符串,而是将所有亚组重新编码,以单独的列呈现在数据中。在案例中,我们感兴趣的是发布状态是否对汇总结果有调节作用。希望对发表在同行评议期刊上的研究与论文进行比较。为此,我们需要为每个亚组创建两个变量/列(同行评审、论文)。在每一列中,根据代码:1 =yes和 0 = no来定义效应值是否属于这个亚组。必须注意的是,亚组编码必须是互斥的。因为如果一项研究同时是“同行评审”组和“论文”组的一部分,我们就无法计算亚组效应。
12.1.2 模型拟合Model fitting
现在开始模型拟合。(我)将之前的全模型结果保存到full.model。模型拟合需要用到metafor包里的rma.mv()函数。该函数有许多参数,如果想要了解具体内容,可以在命令窗口输入帮助函数,即?metafor::rma.mv()。本节我们只需要关注几个重要的参数。rma.mv()函数里random参数里的定义格式和其他使用混合效应模型的包一样,比如lme4(Bateset al., 2015)。格式是单波浪线 “~” ,加竖线“|”,然后将组间变量(groupvaraibles)(如研究,测量方式,区域等等)定义为随机效应。这里组间变量一般称为随机截距(randomintercept),因为它假定我们的模型中每个组间变量有不同的截距。我们之前在多水平模型中有提到,我们有两个组间变量;一个是level2水平,一个是level3水平。假设这些组间变量是嵌套型的(nested),即level2上的几个效应量(用ID_2表示)构成了level3水平的更大的集群(用ID_1表示)。这个设定可以让我们在rma.mv()函数中定义我们的随机变量为嵌套结构。借助斜线 “/” 来区分高阶的和低阶的组间变量。“/” 左边是高水平的变量或集群(这里指代ID_1),“/”右边代表嵌套在高水平下集群下的低一级的变量(这里指代ID_2)。所以,我们的公式就可以写成:~ 1 | ID_1/ID_2full.model <- rma.mv(y, v, random = ~ 1 | ID_1/ID_2, tdist = TRUE, data = mlm.data, method = "REML")
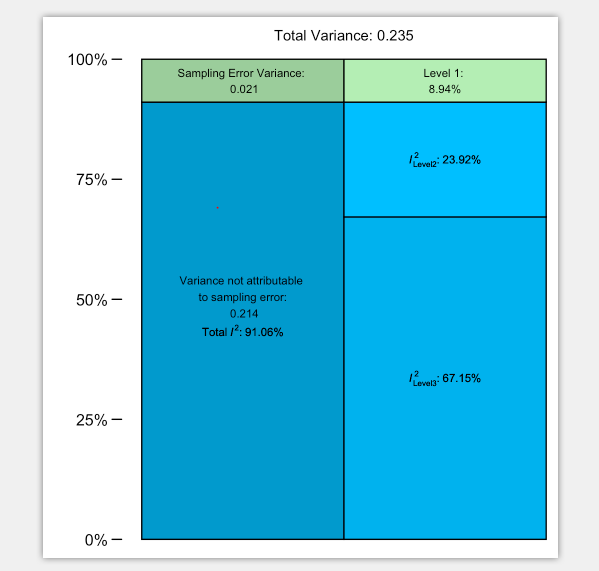
首先,我们看下Variance Components。这里,我们可以看到每一个水平下的变异值,σ21(level3, ID_1), σ22(level 2, 嵌套在ID_1下的ID_2),结果nlvls,可以看到每一个level下的亚组数目(subgroups)。ID_1/ID_2,这里80是因为每一个效应量有各自的ID.Model Results里的estimate可以看到合并效应量的值,等于0.4345。因为我们y里定义的效应量是Hedge’sg,所以这里就是g =0.4345,置信区间为0.20-0.67.Test for Heterogeneity 这里可以看到当前数据集下效应量的变异值非常显著(p<0.0001)。但是这一结果并没有传递多少信息,因为我们感兴趣的是变异值在当前模型里各个水平的分布情况。
12.1.3 方差分布distribution of total variance
正如前文讨论,我们实际感兴趣的部分是方差在建立的模型三个水平上的分布(distribution of variance over the three levles of our model)。Viechtbauer(2019)提供了评估样本方差的公式,即需要计算每个水平上的方差。直接调用dmetar 包里的函数mlm.variance.distribution.该函数在dmetar包里,如果已经安装过这个包,直接加载进来即可。如果不想加载该包,你可以直接运行原函数代码。点击链接下载https://raw.githubusercontent.com/MathiasHarrer/dmetar/master/R/mlm.variance.distribution.R
将链接里的代码复制到一个空的R脚本,保存,回车键运行。注意运行该函数之前确保ggplot2已经加载进当前的工作环境。mlm.variance.distribution(x = full.model)
从图中可以看到level1上有8.94%变异,level2上有23.92%的变异,level3上占据67.15%的变异。其中level2和level3上的变异所占比等同于研究间异致性(between-study heterogeneity) I2 (见第六章内容)。但是,在三水平的元分析时,有三种类型的I2:I2Level2:描述了集群内异质性(within-cluster heterogeneity)的数量;I2Level3:描述了集群间异质性(between-cluster heterogeneity)的数量;I2total:描述了取样误差之外(sampling error)的总异质性(total amount of heterogeneity). I2total数值上等同于level2和level3上异质性之和。
12.1.4 比较拟合性Comparing the fit
当然,在拟合三水平的模型时,我们更感兴趣的是三水平模型是否比二水平的模型更能解释变异性。metafor可以用来比较两模型中去掉了哪个水平。借助rma.mv函数,我们将一个水平的变异设置成常数。这里我们改变sigma2的参数,即设置一个向量,来告诉函数哪一个水平设置成常数值,通用格式是c(level3,level2)。所以我们想将level2设置成常数,其他的保留不变,就可以写成sigma2=c(NA,0)。反之可以将level3设置成常数。model.l2.removed<-rma.mv(y, v, random = ~ 1 | ID_1/ID_2, tdist = TRUE, data = mlm.data, method = "REML", sigma2 = c(NA, 0))summary(model.l2.removed)
上图展示的结果中Model Results部分可以看到没有变化,但是水平2是否真的概括了数据中的变异了吗?我们可以借助anova()函数来比较全模型(full.model)和去掉水平2的模型(model.l2.removed).方法和结果如下:
anova(full.model, model.l2.removed)
我们可以看到,相比较降低水平的模型,全模型的确更能拟合原始数据,即Akaike Information Criterion(AIC)和Bayesian Information Criterion (BIC)的值在全模型中都较低,并且差异显著(p<0.0001)。这就说明去掉一个水平的模型是合理的。现在我们来看一下,如果将level3设置成常数,结果如何。
model.l3.removed<-rma.mv(y, v, random = ~ 1 | ID_1/ID_2, tdist = TRUE, data = mlm.data, method = "REML", sigma2 = c(0, NA))summary(model.l3.removed)
从结果中可以看到,相比较全模型来说,三水平模型也很有用。
12.2三水平模型的组间分析Subgroup Analyses in Three-Level Models
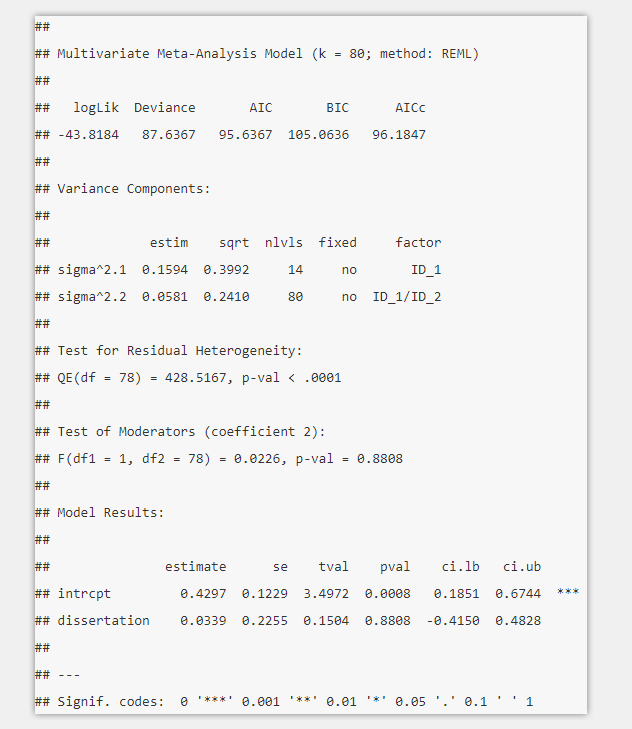
建立完三水平的元分析模型(three-level meta-analytic model)之后,我们可以对调节变量(moderator)的整体效应量(overall effect)进行检验,例如进行组间分析(subgroup analyses)。在R语言中,我们可以通过指定ram.mv()函数的输入参数mods来实现检验。在该函数中,mods参数在赋值之前应添加一个前置符号“~”,在样例中即mods = ~ dissertation。完整示例如下:model.mods<-rma.mv(y, v, random = ~ 1 | ID_1/ID_2, tdist = TRUE, data = mlm.data, method = "REML", mods = ~ dissertation)summary(model.mods)
其中,最重要的输出结果是Test of Moderators。我们可以看到统计检验值F1,78 =0.0226, p=0.8808,说明小组之间没有显著差异。另一个输出参数为Model Results,它呈现出的是一个元回归框架表(within a meta-regression framework),该表格中的参数并非直接等于效应量,而是需要公式计算(如下图)。其中,第一行intrcpt参数(截距intercept),它代表的是当dissertation=0时g的取值,即同行评议文章的值。而第二行预测变量dissertation的估值可以理解成斜率(slope)。而整体效应量应等于截距(intercept)加上斜率(slope),公式如下。即: