539 阅读 2020-09-20 09:17:02 上传
以下文章来源于 神经语用学

一、主成分分析Principal Component Analysis,PCA

1. 概念
主成分分析是利用降维(线性变换)的思想,在损失很少信息的前提下把多个指标转化为几个不相关的综合指标(主成分),即每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能(主成分必须保留原始变量90%以上的信息),从而达到简化系统结构,抓住问题实质的目的。
Ps:这里90%标准的说法并不统一
如何衡量信息的含量,经典的做法就是采用“方差”来表示。F1(第一主成分)的方差越大,F1所包含的信息就越多。这样,F1的选取方法是,在所有的原来p个变量(指标)的线性组合中,选取方差最大的线性组合作为F1,称为第一主成分。第二、第三主成分以此类推。
2. 什么是降维
降维处理是将高维数据化为低维度数据的操作。
意义:①在原始的高维空间中,包含有冗余信息以及噪音信息,在实际应用中造成了误差,降低了准确率;而通过降维,我们希望减少冗余信息所造成的误差,提高精度。 ②又或者希望通过降维算法来寻找数据内部的本质结构特征。
下面是简单的二维降到一维的例子。
比如我们有一些关于房子的单价和面积的数据。
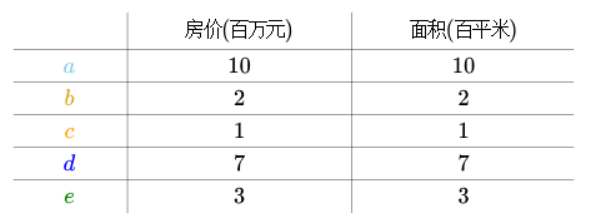
我们将它中心化变成下图
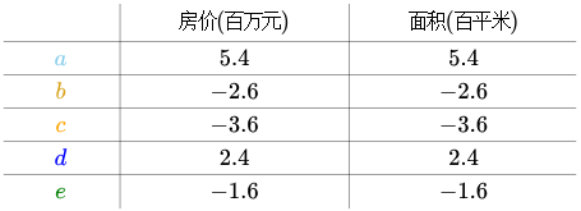
将它放入直角坐标系中
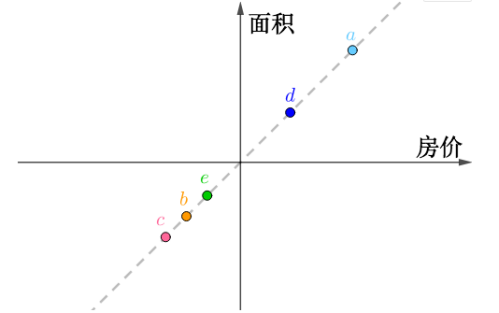
旋转坐标系使其契合
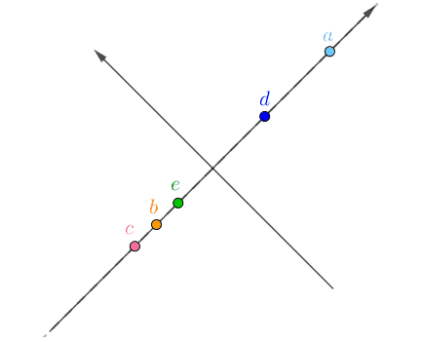
旋转后的坐标系,横纵坐标不再代表“房价”、“面积”了,而是两者的是线性组合,这里把它们称作“主元1”、“主元2”,坐标值很容易用勾股定理计算出来。
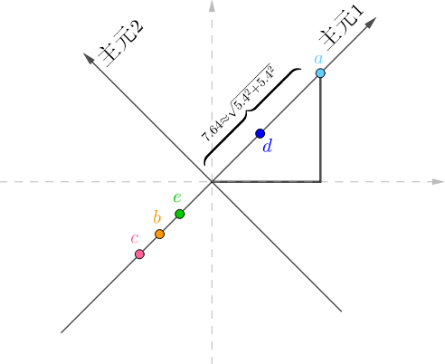
最后删去无用的“主元2”

这是一个理想情况的例子,刚好主元2都是0,只要主元1就够了,这样就又把数据降为了一维,而且没有丢失任何信息。
3. 主成分分析的计算过程
对原始数据进行标准化处理,消除量纲
计算标准化数据的相关系数矩阵
计算标准化数据的相关系数矩阵的特征根及对应的特征向量
选出最大的特征根,对应的特征向量等于第一主成分的系数;选出第二大的特征根,对应的特征向量等于第二主成分的系数;以此类推
计算累积贡献率,选择恰当的主成分个数;
解释主成分:写出前k个主成分的表达式
确定各样本的主成分得分
根据主成分得分的数据,做进一步的统计分析

二、探索性因子分析Exploratory Factor Analysis,EFA

1. 概念
因子分析是将多个实测变量转换为少数几个不相关的综合指标的多元统计方法。它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。假想变量是不可观测的潜在变量,称为因子。
假定这是p个有相关关系的随机变量含有m个彼此独立的因子,可表示为
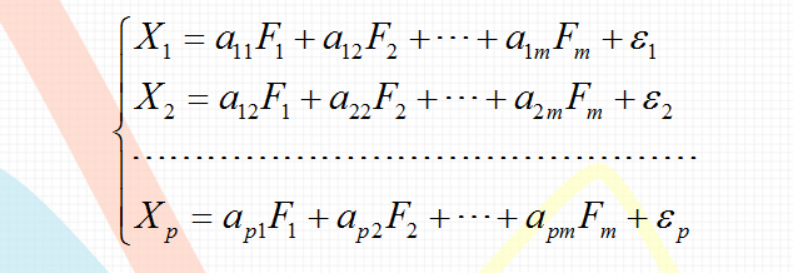
2. 数据是否适合做因子分析
因子分析前,首先进行KMO检验和Bartlett's球形检验。
KMO检验用于检查变量间的相关性和偏相关性,取值在0~1之间。KMO统计量越接近于1,变量间的相关性越强,偏相关性越弱,因子分析的效果越好。实际分析中,KMO统计量在0.7以上时效果比较好;当KMO统计量在0.5以下,此时不适合应用因子分析法,应考虑重新设计变量结构或者采用其他统计分析方法。
Bartlett's球形检验主要看p值。
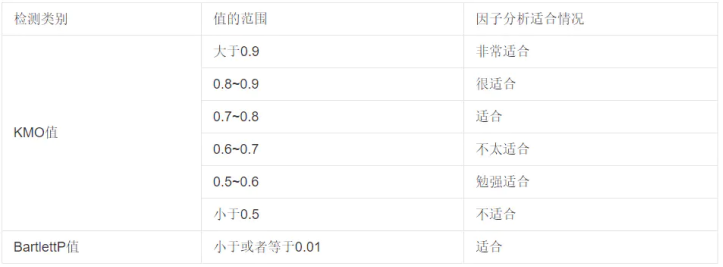
3. 探索性因子分析的计算过程
将原始数据标准化,以消除变量间在数量级和量纲上的不同。
求标准化数据的相关矩阵。
求相关矩阵的特征值和特征向量。
计算方差贡献率与累积方差贡献率。
确定因子:设F1,F2,…,Fp为p个因子,其中前m个因子包含的数据信息总量(即其累积贡献率)不低于80%时,可取前m个因子来反应原评价指标。
因子旋转:若所得的m个因子无法确定或其实际意义不是很明显,这时需将因子进行旋转以获得较为明显的实际意义。
附上一张主成分分析和因子分析的流程图
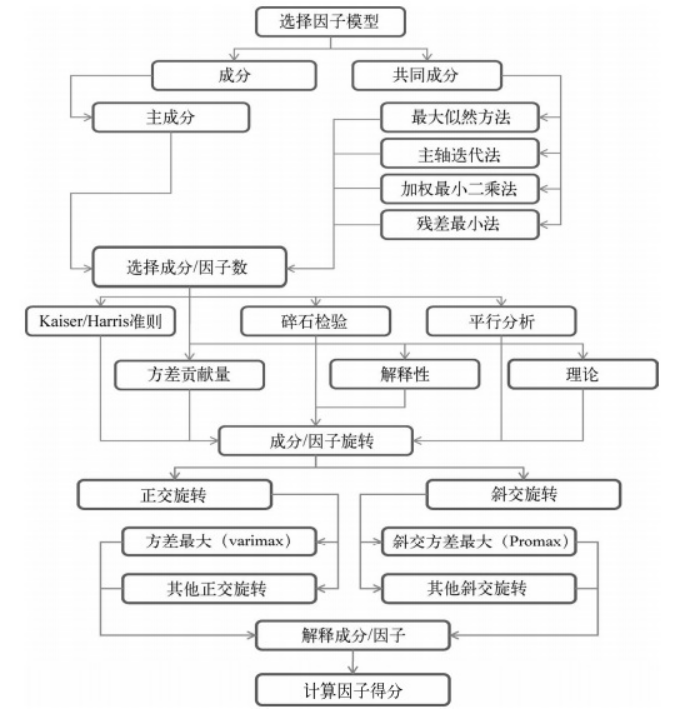

三、区别与联系

1. 联系
都对原始数据进行标准化处理;
都消除了原始指标的相关性对综合评价所造成的信息重复的影响;
构造综合评价时所涉及的权数具有客观性;
在信息损失不大的前提下,减少了评价工作量。
2. 区别
1
2.1 原理不同
主成分分析基本原理:利用降维(线性变换)的思想,在损失很少信息的前提下把多个指标转化为几个不相关的综合指标(主成分),即每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能(主成分必须保留原始变量90%以上的信息),从而达到简化系统结构,抓住问题实质的目的。
因子分析基本原理:利用降维的思想,由研究原始变量相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量表示成少数的公共因子和仅对某一个变量有作用的特殊因子线性组合而成。就是要从数据中提取对变量起解释作用的少数公共因子(因子分析是主成分的推广,相对于主成分分析,更倾向于描述原始变量之间的相关关系)。
2
2.2 线性表示方向不同
因子分析是把变量表示成各公因子的线性组合;
主成分分析中则是把主成分表示成各变量的线性组合。
3
2.3 假设条件不同
主成分分析:不需要有假设(assumptions);
因子分析:需要一些假设。因子分析的假设包括:各个共同因子之间不相关,特殊因子(specificfactor)之间也不相关,共同因子和特殊因子之间也不相关。
4
2.4 求解方法不同
求解主成分的方法:从协方差阵出发(协方差阵已知),从相关阵出发(相关阵R已知),采用的方法只有主成分法。(实际研究中,总体协方差阵与相关阵是未知的,必须通过样本数据来估计)
求解因子载荷的方法:主成分法,主轴因子法,极大似然法,最小二乘法,a因子提取法。
5
2.5 解释重点不同
主成分分析:重点在于解释个变量的总方差,
因子分析:则把重点放在解释各变量之间的协方差。
6
2.6 算法上的不同
主成分分析:协方差矩阵的对角元素是变量的方差;
因子分析:所采用的协方差矩阵的对角元素不在是变量的方差,而是和变量对应的共同度(变量方差中被各因子所解释的部分)。
7
2.7 优点不同
因子分析:
对于因子分析,可以使用旋转技术,使得因子更好的得到解释,因此在解释主成分方面因子分析更占优势;其次因子分析不是对原有变量的取舍,而是根据原始变量的信息进行重新组合,找出影响变量的共同因子,化简数据。
主成分分析:
如果仅仅想把现有的变量变成少数几个新的变量(新的变量几乎带有原来所有变量的信息)来进入后续的分析,则可以使用主成分分析,不过一般情况下也可以使用因子分析。
通过计算综合主成分函数得分,对客观经济现象进行科学评价。
它在应用上侧重于信息贡献影响力综合评价。
应用范围广,主成分分析不要求数据来自正态分布总体,其技术来源是矩阵运算的技术以及矩阵对角化和矩阵的谱分解技术,因而凡是涉及多维度问题,都可以应用主成分降维。
8
2.8 应用场景不同
主成分分析:
可以用于系统运营状态做出评估,一般是将多个指标综合成一个变量,即将多维问题降维至一维,这样才能方便排序评估;此外还可以应用于经济效益、经济发展水平、经济发展竞争力、生活水平、生活质量的评价研究上;主成分还可以用于和回归分析相结合,进行主成分回归分析,甚至可以利用主成分分析进行挑选变量,选择少数变量再进行进一步的研究。一般情况下主成分用于探索性分析,很少单独使用,用主成分来分析数据,可以让我们对数据有一个大致的了解。
几个常用组合:主成分分析+判别分析,适用于变量多而记录数不多的情况;主成分分析+多元回归分析,主成分分析可以帮助判断是否存在共线性,并用于处理共线性问题;主成分分析+聚类分析,不过这种组合因子分析可以更好的发挥优势。
因子分析:
首先,因子分析+多元回归分析,可以利用因子分析解决共线性问题; 其次,可以利用因子分析,寻找变量之间的潜在结构;再次,因子分析+聚类分析,可以通过因子分析寻找聚类变量,从而简化聚类变量; 此外,因子分析还可以用于内在结构证实。

四、如何在R中实现

我们主要用到的是psych包。
该包函数用法具体如下。

下面是具体代码
install.packages('psych')
library(psych)
#导入数据 这一份数据是我国31个地区某一年的社会经济发展数据,
#其中17个指标分别包括GDP、人均GDP、人均社会消费品零售额、人均货运总量、科研经费占GDP比重等
library (readxl)
data <- read_excel('economy.xlsx')
#使用fa.parallel()函数绘制碎石图
#data为待研究的数据集或相关系数矩阵 data[,-1]为去掉第一列数据 data[-1,]为去掉第一行数据
#fa为主成分分析(fa= "pc")或者因子分析(fa = "fa")
#n.iter指定随机数据模拟的平行分析的次数。
#show.legend显示图例
fa.parallel (data[,-1],fa='pc',n.iter = 100,show.legend = FALSE)
下面是生成的碎石图
#使用principal()函数提取相应的主成分
# data:相关系数矩阵或原始数据矩阵
# nfactors:设定主成分数
# rotate:指定旋转的方法(默认最大方差旋转(varimax))
# scores:设定是否需要计算主成分得分(默认不需要)
# 由于PCA只对相关系数矩阵进行分析,在获取主成分前,原始数据将会被自动转换为相关
data_pca <- principal(data[,-1],nfactors = 2,rotate = "none")
data_pca

#PC1与PC2栏为成分载荷,它是指观测变量与主成分的相关系数,
#从上表中我们可以看到,第一主成分与X2、X4、X6等变量高度相关,第二主成分与X1、X9等变量相关。
#h2栏指成分公因子方差,即主成分对每个变量的方差解释度。
#对于X2,两个主成分一共解释了96%的方差
#u2栏指成分唯一性,即方差无法被主成分解释的比例(1–h2)。
#SS loadings行包含了与主成分相关联的特征值,指的是与特定主成分相关联的标准化后的方差值。
#Proportion Var行表示的是每个主成分对整个数据集的解释程度,
#在这一案例中,第一主成分解释了65%的方差,第二主成分解释了16%,两者总共解释了81%的方差。
#使用ggfortify包autoplot()函数绘制主成分分析图
install.packages('ggfortify')
library(ggfortify)
df <- data[,-1]
autoplot(prcomp(df,scale=TRUE),colour='green',label=TRUE)

下面是因子分析的R代码
#因子分析
#导入数据
library(openxlsx)
data <- read.xlsx('')
#KMO检验和Bartlett's球形检验
cortest.bartlett(data)
KMO(data)
# 计算相关系数矩阵
cor(data)
#提取公共因子
library(psych)
cor_data <- cor(data)
# fa="both":同时展示主成分分析和因子分析的结果 n.obs是观测数
fa.parallel(cor_data, n.obs=112, fa="both", n.iter=100)
#使用fa()函数进行因子提取 这里我们选用主轴迭代法进行未旋转因子的提取
#具体参数介绍
# r:相关系数矩阵或原始数据矩阵,
# nfactors:设定主提取的因子数(默认为1)
# n.obs:观测数(输入相关系数矩阵时需要填写)
# rotate:设定旋转的方法(默认互变异数最小法)
# scores:设定是否需要计算因子得分(默认不需要)
# fm:设定因子化方法(默认极小残差法)
fa_model <- fa(cor_data,nfactors = 4,rotate = 'none',fm='pa')
fa_model
#因子旋转 正交旋转法
fa_model_varimax <- fa(cor_data,nfactors = 4,rotate = 'varimax',fm='pa')
fa_model_varimax
#对因子旋转结果进行可视化展示 散点图
factor.plot(fa_model_varimax)
#因子之间的相关系数图
# simple = TRUE:仅显示每个因子下最大的载荷,以及因子间的相关系数
fa.diagram(fa_model_varimax,simple = FALSE)