零假设显著性检验（NHST）是目前社会科学研究数据分析的主要工具。但是在统计学领域，NHST受到了广泛的批评。越来越多的统计学者提倡使用贝叶斯方法检验研究假设，也经常有做实证研究的学者咨询如何使用贝叶斯因子(Bayes factor, BF)进行数据分析。本文首先介绍贝叶斯因子的相关问题，随后展示如何使用R软件包bain进行贝叶斯检验。
贝叶斯因子简介
1什么是贝叶斯因子？
贝叶斯因子是贝叶斯假设检验指标。以零假设H0与备择假设Hu为例，贝叶斯因子BF0u量化了数据在假设H0下比在假设Hu下更有可能被观测到的程度，换言之，BF0u衡量了H0相对于Hu受到数据支持的程度。比如BF0u = 5表示数据对H0的支持程度是Hu的5倍。

                                              2贝叶斯因子的优势

通过对比基于p值的NHST，来说明贝叶斯因子的优势。
1). NHST常以 p＜0.05作为统计推断的依据（或给定显著性水平0.05，统计量是否落入拒绝域）。但是，为什么是 p＜0.05，不是0.06或0.04？ p＜0.05是一种约定俗成，并无严格的统计理论依据。研究者通常希望得到 p＜0.05的结果以证明研究理论。

贝叶斯因子表示数据支持假设的相对程度。显然，BF0u ＞1，数据更支持零假设；BF0u ＜1，数据更支持备择假设。因此，BF0u ＝1是贝叶斯因子天然的分割。同时，贝叶斯因子存在不决定区间(indecision region)，不作二分（拒绝或不拒绝）判断。
2). NHST是在假定零假设为真的前提下进行的，因此无法接受零假设。研究者通常误用p＞0.05来证实无差异的研究理论。而贝叶斯因子可以得到支持或反对零假设的证据。
3). NHST不能同时比较多个假设。而贝叶斯因子可以转化为后验模型概率(posterior model probability)，以百分比的形式表达哪个研究假设受到数据支持更多，找出最优理论。

               
4). NHST不具备连贯性和一致性(coherence and consistency)。当零假设为真时，样本量的增大不会使p值趋于1。而贝叶斯因子具备连贯性与一致性。当零假设为真（或假）时，随着样本量的增大，BF0u趋向于无穷（或0）。
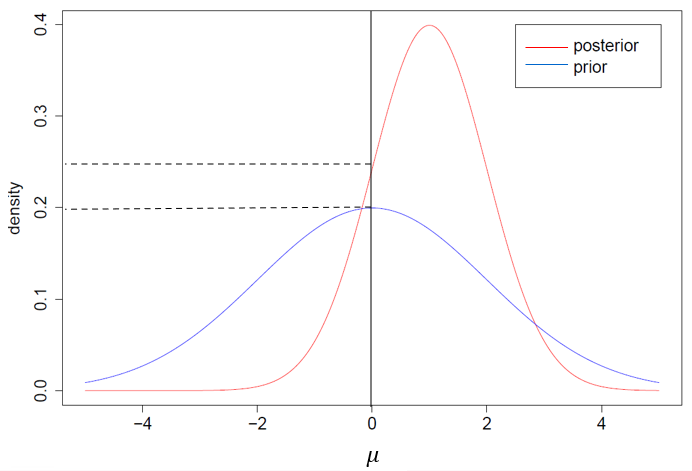
5). NHST只针对一次数据分析。而贝叶斯因子可以通过数据的不断收集而更新。当贝叶斯因子无法明确选择假设时，可继续收集收据，直到得到有说服力的贝叶斯因子。如下图所示，贝叶斯因子随着数据的收集而变化。

                 3贝叶斯因子的阈值
研究者经常问的一个问题是BF0u多大或多小时，将接受或拒绝零假设。这个问题的背后是对阈值根深蒂固的需求，如NHST中

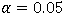
可以决定是否拒绝零假设。然而与NHST不同，贝叶斯因子一般不作二分(拒绝或不拒绝)判断，而是量化假设受数据支持的程度。如果BF0u在1附近，则对零假设或备择假设均没有偏好，即贝叶斯因子是非决定的，需要更多的数据来证明哪个假设是正确的。另一个更直接的问题是，贝叶斯因子应该多大 (或多小)时，期刊会接受文章发表？早在1961年，Harold Jeffreys就给出了BF0u＞3.2或BF0u＜1/3.2，表明数据有正面的证据支持假设H0或Hu。Kass & Raftery (1995) 则建议使用BF0u＞3或BF0u＜1/3来表示数据支持H0或Hu，但需要注意的是，这些阈值同样没有严格的理论依据。我们更推荐不设置阈值，根据贝叶斯因子研究者可做出H0受到数据支持的程度是Hu的x倍的推断结论。
4零假设的替代

一些统计学者认为，零假设太过精确以至于不可能成立(Cohen, 1994; Royal, 1997)，因此，即使没有数据零假设也该被拒绝。此外，很多时候零假设不能准确描述研究理论，比如很难找到两个总体均值是完全相等的。鉴于此，研究者同样可以构造区间假设、次序假设、约等假设来更精确的描述研究理论：

5贝叶斯因子的计算
数学上，贝叶斯因子等于两个假设下数据边缘似然函数的比值。对于零假设与备择假设，贝叶斯因子表示的支持度是通过平衡H0和Hu的相对拟合度(fit)和相对复杂度(complexity)来确定的。简单来说，贝叶斯因子可表示为  

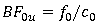
在实际使用中，已有很多软件能够实现贝叶斯因子的计算，包括R 包BayesFactor，bain, BFpack, bayestestR等，其中BayesFactor和bain包可在JASP可视化统计分析软件中通过点击的方式完成数据分析。
 

                               
6先验分布的设置

先验分布反应数据收集前，研究者对模型参数的认知。先验分布对贝叶斯因子的影响很大，因此在贝叶斯检验中，先验分布的设定尤其重要。先验设定可分为主观的和客观的。主观先验基于历史数据或专家经验给出模型未知参数的分布。客观先验可以是无信息的，也可以基于样本数据(如empirical Bayes; posterior prior)。但在贝叶斯检验中，研究者不能设定无信息先验，否则将会产生Lindley悖论，即无论数据如何，零假设都将受到贝叶斯因子的支持。因此，当参数先验信息不存在或研究者不希望引入先验信息以得到完全客观的统计推断结论时，贝叶斯检验通常使用默认的客观先验。贝叶斯检验的默认先验包括g priors, Jeffreys-Zellner-Siow priors, intrinsic priors, fractional priors。默认先验需设定超参数以便根据样本量、参数个数等调整先验分布的尺度。下表列出了四种默认先验及其常用超参数和软件实现。

7贝叶斯因子的应用
贝叶斯因子在检验零假设，区间假设，次序假设，变量选择等方面已有广泛的应用，也有诸多实证研究使用贝叶斯因子分析数据。详见最新一篇关于贝叶斯因子应用的述评

https://psyarxiv.com/cu43g
bain软件包教程
bain是BAyesian INformative hypotheses evaluation的简称。R软件包bain的主要功能是通过计算贝叶斯因子，评估研究者的理论。bain使用部分样本数据构造先验分布，给出完全客观的贝叶斯检验结果，研究者不再需要考虑先验分布的选取问题。
目前bain软件包可处理的统计模型包括t检验（one sample t test; two samples t test; Welch’s t test; paired samples t test），等效性检验(equivalence test)；方差分析(ANOVA)，协方差分析(ANCOVA)，多重回归(multiple regression)，重复测量(repeated measures)，逻辑回归(logistic regression)，结构方程模型(包括验证性因子分析confirmatory factor analysis，潜变量回归latent regression等)，同时可处理多组数据与缺失数据。bain软件包可在R语言平台和JASP软件平台(0.11.1及以后版本)中实现。   R软件包bain的用法如下：

library(bain) #加载包

bain(x, hypothesis, ...)
其中x表示检验模型对象，可为t检验x<-t_test()，线性回归x<-lm()，结构方程模型x<-sem()等输出结果。hypothesis为待检验的研究假设，如

hypotheses <- "a > b > c & b > 0; a = b = c = 0"
指定了两个研究假设，a, b, c为所关心的模型参数，符号&用于连接假设中的限制条件，符号;用于区分不同假设。同时比较多个假设(模型)时，可将不同假设(模型)以;号区分。 
给定模型x和假设hypothesis，运行bain函数可得到每个待检验假设或模型的拟合度(Fit)，复杂度(Com), 与备择假设相比的贝叶斯因子(BF.u)，与补充假设相比的贝叶斯因子(BF.c)，以及假设或模型的后验概率(PMP)。
 

下面我们使用bain的built-in数据sesamesim，以方差分析、回归模型、和验证性因子分析为例来具体介绍。
1方差分析
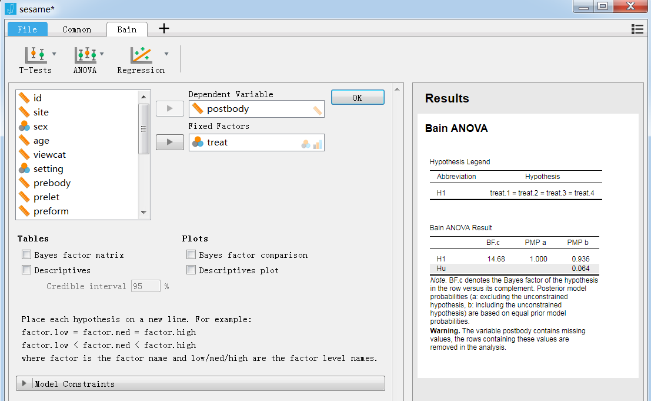
选取sesamesim数据中的postnumb为因变量，site为分组变量，方差分析的待检验假设为各组postnumb相等vs各组大小关系为组2>组5>组1>组3>组4，R语言代码如下：

sesamesim$site <- as.factor(sesamesim$site) #make factor variableanov <- lm(postnumb ~ site - 1, sesamesim) #anova using lm()result <- bain(anov, hypothesis = "site1=site2=site3=site4=site5;site2>site5>site1>site3>site4") #test检验输出结果如下

            由上述结果可知假设H1（与备择假设Hu相比）的贝叶斯因子BF1u=0，因此数据不支持各组postnumb相等；假设H2的贝叶斯因子为BF2u=16.013，即数据支持各组大小关系为2>5>1>3>4的研究理论。此外，我们可以得到假设H1，H2与Hu的后验模型概率PMPb，可知H2收到数据支持的程度最高（后验模型概率为0.941）。
2线性回归
选取sesamesim数据中的postnumb为因变量，age, peabody, prenumb为自变量，待检验假设为prenumb的效应强于peabody强于age。R语言代码如下:

regr <- lm(postnumb ~ age + peabody + prenumb, sesamesim) #regressionresult<-bain(regr, "prenumb>peabody>age", standardize = T) #test检验结果如下

需注意的是，比较回归效应(系数)时，应对回归系数进行标准化处理，即指定standardize = T。由上述结果可知假设H1:prenumb>peabody>age的贝叶斯因子为BF1u=5.769，即数据支持待检验假设的证据是备择假设的5.769倍。
3验证性因子分析
R软件包bain检验结构方程模型参数需借助软件包lavaan。选取sesamesim数据中Ab, Al等指标测量A因子; Bb, Bl等指标测量B因子。待检验假设为所有因子载荷均大于0.6。R语言代码如下：

library(bain)library(lavaan)# Specify and fit the confirmatory factor modelmodel <- '    A =~ Ab + Al + Af + An + Ar + Ac    B =~ Bb + Bl + Bf + Bn + Br + Bc'# Use the lavaan sem function to execute the confirmatory factor analysisfit <- sem(model, data = sesamesim, std.lv = TRUE)

# Formulate hypotheses, call bain, obtain summary statshypotheses <-"A=~Ab>.6 & A=~Al>.6 & A=~Af>.6 & A=~An>.6 & A=~Ar>.6 & A=~Ac>.6 &B=~Bb>.6 & B=~Bl>.6 & B=~Bf>.6 & B=~Bn>.6 & B=~Br>.6 & B=~Bc>.6"result <- bain(fit, hypotheses, standardize=TRUE)sr <- summary(result, ci = 0.95)上述代码前半部分利用lavaan软件包中的sem()函数定义了验证性因子分析模型。后半部分使用sem()输出结果与指定的假设在bain()函数中计算贝叶斯因子。其中A=~Ab表示Ab对于因子A的载荷。计算结果如下：

                          由上述结果可知假设“所有因子载荷均大于0.6”的贝叶斯因子为BF.u=94.273，表明得到数据的支持。同时结果给出了因子载荷估计值与95%可信区间。
更多模型实例与用法请见：https://cran.r-project.org/web/packages/bain/vignettes/Introduction_to_bain.html软件包bain仍在持续开发更多模型与功能，欢迎大家关注与使用。以下是关于bain的参考文献，有贝叶斯因子统计方法的如Gu et al. (2018)，有贝叶斯因子应用的如Gu et al. (2020)，有介绍bain的使用教程如Hoijtink et al. (2019a)和Van Lissa et al. (2020)。
ReferencesVan Lissa, C.J., Gu, X., Mulder, J., Rosseel, Y., van Zundert, C, & Hoijtink, H. (2020). Teacher’s corner: Evaluating informative hypotheses using the Bayes factor in structural equation models. Structural Equation Modelling-A Multidisciplinary Journal. Doi: 10.1080/10705511.2020.1745644.Gu, X., Hoijtink, H., & Mulder, J. (2020). Bayesian one-sided variable selection. Multivariate Behavioral Research. DOI: 10.1080/00273171.2020.1813067.Hoijtink, H., Mulder, J., van Lissa, C., & Gu, X. (2019). A tutorial on testing hypotheses using the Bayes factor. Psychological Methods, 24, 539-556. DOI: 10.1037/met0000201Hoijtink, H., Gu, X.,& Mulder, J. (2019). Bayesian evaluation of informative hypotheses for multiple populations. British Journal of Mathematical and Statistical Psychology, 72, 219-243. DOI: 10.1111/bmsp.12145Hoijtink, H., Gu, X., Mulder, J., & Rosseel, Y. (2019). Computing Bayes factors from data with missing values. Psychological Methods, 24, 253-268. DOI: 10.1037/met0000187.Gu, X., Mulder, J., & Hoijtink, H. (2018). Approximate adjusted fractional Bayes factors: A general method for testing informative hypotheses. British Journal of Mathematical and Statistical Psychology, 71, 229-261. DOI: 10.1111/bmsp.12110.

END